Skip to content

Latest commit

 

History

History
475 lines (411 loc) · 21.7 KB

Datastructures_Alogrithams.md

File metadata and controls

475 lines (411 loc) · 21.7 KB

Data Structures and Algorithams

Table of Contents

Algorithams

An algorithm - Is a set of well-defined instructions to solve a particular problem. It takes a set of input and produces a desired output

  • Input
  • Output
  • Definiteness - It must be clear
  • Finiteness - It must stop
  • Effectiveness - some purpose How to Analyse Alogithm
  1. Time - must be Time efficient
  2. Space - must be memory effficient
  3. N/W -
  4. Power -
  5. CPU Registers - Every statement/line is 1 unit of time Frequency Count Method

  • Means, the number of times the statement is executed in the program

  • To calculate the time, consider the degree

    - sum(a,b)       => f(n) = 2n +3                  => O(n)
- add(a,b,n)        => f(n) = 2n2 + 2n + 1           => O(n2)
- multiply(a,b,n)   => f(n) = 3n3 + 3n2 + 2n + 1    => O(n3)

  • To Calculate space complexity, consider all variables

    - sum(a,b)      => s(n) = n+3        => O(n)
- add(a,b,n)  => s(n) = 3n2 + 3    => O(n2)
- multiply(a,b,n) => s(n) = 3n2 +4     => O(n2)

Time Complexity Examples

- for(i=0;i<n;i++)          => O(n)
- for(i=n;i>0;i--)          => O(n)
- for(i=0;i<n;i=i+2)    n/2 => O(n)
- for(i=0;i<n;i++) 
    for(j=0;j<i;j++)        => O(n^2)
- for(i=1;i<n; i=i++) 
  for(j=0;j<n;j++)          =>O(n^2)
- p=0
  for(i=0;p<=n;i++)         =>O(root N)

- for(i=1;i<n; i=i*2)       => O(log n base 2)
- for(i=1;i<n; i=i*3)       => O(log n base 3)
- for(i=n;i>1; i=i/2)       => O(log n base 2 )

- for(i=0;i*i<n;i++)        => O(root n)

- for(i=0;i<n;i++)          => O(n)
    stmt
  for(j=0;j<i;j++) 
    stmt                    
- p=0
  for(i=0;i<n;i*2)          => O(log log n)
    stmt
  for(j=0;j<p;j*2) 
 stmt                       

- for(i=0;i<n;i++)          =>O(nlogn)
    stmt
  for(j=0;j<i;j=n*2) 
 stmt

Big O noation is for...

  • Time Complexity (how much runtime it will take)
  • Space Complexity (how much memory it will take)

Types of Time Complexities (Classes of Funcitons)

  • Constant Time Complexity - O(1)
  • Linear Time Complexity - O(n)
  • Logarithmic Time Complexity - O(log n)
  • Quadratic Time Complexity - O(n ** 2)
  • Cubic Time Complexity - O(n ** 3)
  • Exponential Complexity - O(2 power n)

How to calculate Time Complexities

  • Mathematical way
  • Programatic or Practical way
    1. Find the Fast increasing term
    2. Remove the cofficient in that term

Compare Class of Functions

1 < log n < √n < n < n log n < n2 < n3 ... 2n < 3n < Nn < O(1) < O(logN) < O(N) < O(NlogN) < O(N^2) < O(2^N)< O(N!)

Log Values

  • Logn n = 1
  • logn 1 = 0
=> log(1) = 0  
=> log(2) = 1 
4 => 2 power 2                => log2(4)  =2
8 => 2 power 3                => log2(8)  =3  
16 => 2 power 4               => log2(16) =4
1024 => 2 power 10            => log2(1024)=10
4,294,967,296 => 2 power 10   => log2(~4B)=32

Asymptotic Notations - Big Oh

  1. BigO Upper bound (f(n) <= BigO(n) )
  2. Omega Lower bound (f(n) >= Omega(g(n) )
  3. Theta Average bound (f(n) = Theta(n) )
  • BigO or Omega is when we are not sure
  • Theta gives best
  • IF Theta can't find, go for BigO or Omega

Data Structures

Data Structures are way storing and organizing data in a computer for efficient access and modification

Array

  • Linear DS; in Python using List
  • Similar data types - Stores data as contiguous memory locations

Linked List

  • Linear DS, in Python using List

  • Stores as individual nodes and has pointers to next node

  • Singly-linked list:

    • linked list in which each node points to the next node
    • the last node points to null
    representing linked list by connecting each node with next node using address of next node

  • Doubly-linked list:

    • linked list in which each node has two pointers, p and n, such that p points to the previous node and n points to the next node;
    • the last node's n pointer points to null
    doubly linked list

  • Circular-linked list:

    • linked list in which each node points to the next node
    • the last node points back to the first node
    circular linked list

  • Time Complexity:

    • Access: O(n)
    • Search: O(n)
    • Insert: O(1)
    • Remove: O(1)

  • Diff

    • For LL No need to allocate momory
    • LL Insertion is easy
    • LL Memory is higher (p & n)
    • Insertion/Delete at begining = O(1)
    • Insert/Delete at end = O(n)

Stack

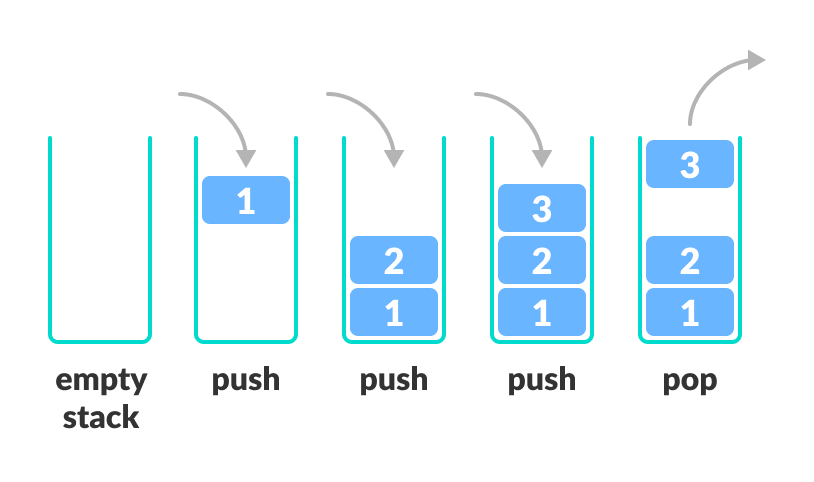
  • Linear DS, Last In First Out operation;

    • push - Insert at end
    • pop - remove at end
    • isEmpty - check stack empty
    • isFull - check if stack is full
    • peek - get the vale of top element (without remove)

  • In python using List/collections.deque/queue.LifoQueue

  • Time Complexity

    • Push: Insert - O(1)
    • Pop: Delete - O(1)
    • Search - O(n)
    represent the LIFO principle by using push and pop operation

Queue

  • Linear DS, First In First Out operation;

    • push - Insert at end
    • pop - remove at start

  • In python using List/collections.deque/queue.LifoQueue

  • Time Complexity

    • Push: Insert - O(1)
    • Pop: Delete - O(1)
    • Search - O(n)
    Representation of Queue in first in first out principle ### Hashmap/Hashtable

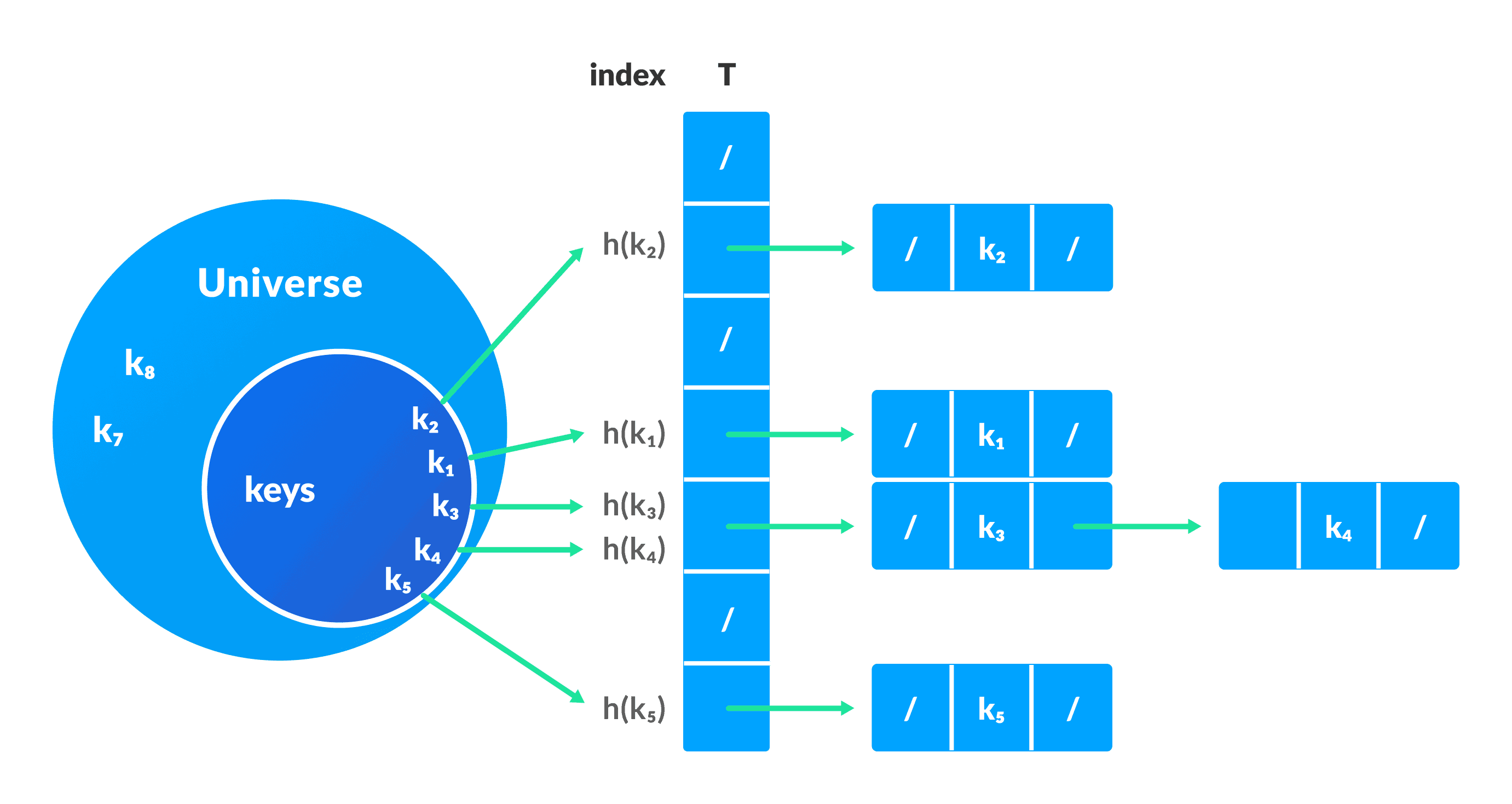
  • Hashing

    • assigning an object into a unique index called as key.
    • Object is identified using a key-value pair
    • Dictionary - collection of objects

  • Hash table storing elements as key-value pairs, identify using key

  • Hash table memory efficient

  • Lookp/Insertion/Deletion Complexity is using key always O(1)

  • Collision: if hash function generetes same function the conflict called Collision.

    • Chaining - one key, store values as List in dictionary
      chaining method used to resolve collision in hash table
    • Open Addressing - Linear/Quadratic Probing and Double Hashing
      • Linear Probing - collision is resolved by checking the next slot
      • Quadratic Probing- similar to linear probing but the spacing between the slots is increased
      • Double hashing - applying a hash function & another hash function

  • Time Complexity:

    • Lookp/Insertion/Deletion is using key always O(1)

  • Tree

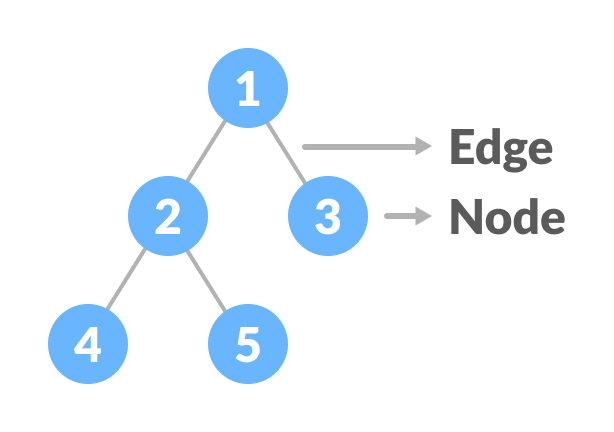
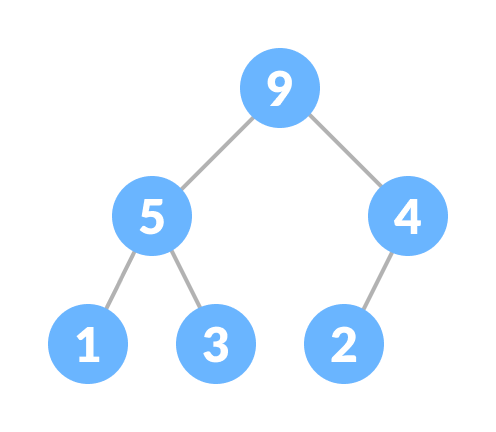
    • A Tree is Non Linear DS, hierarchical, undirected, connected, acyclic graph
      • Root - top most node of a tree.
      • Node - data and pointers to another node
      • Edge - link between nodes
      • leaf nodes(L1, L2, L3)
      Nodes and edges of a tree
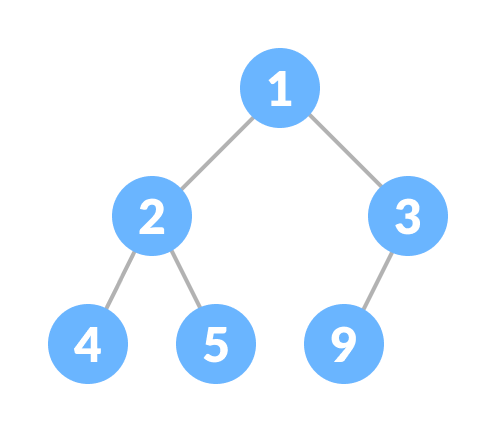
    • Binary Tree
      • parent node can have at most two children
      • Left node has lesser numbers
      • Right node has greater numbers
      • Full Binary Tree - a tree in which every node has either 0 or 2 children
        Full binary tree
      • Perfect Binary Tree - binary tree with exactly 2 child nodes at all level
        Perfect binary tree
      • Complete Binary Tree - every level must be filled L & R, leaf node only lean towards left
        Complete Binary Tree
      • Pathological Binary Tree - tree having a single child either left or right
        Degenerate Binary Tree
      • Skewed Binary Tree - tree is either dominated by the left Pathological nodes or the right Pathological nodes
        Skewed Binary Tree
      • Balanced Binary Tree - difference between the height of the left and the right is either 0 or 1
        Balanced Binary Tree
    • Binary Search Tree
      • Left subtree has lesser numbers,
      • Right subtree has greater numbers
      • BST every node has max 2 nodes
      • Every Iteration we reduce space by half(1/2))
      • if n=8 & 3 iterations, log 8 = 3 => O(log(n))
      • Access, Insert, Search adn Delete = Θ(log(n))
      • delete process
        • if bst not empty => search for node => check node children
        • delete node with children 0; simpley delete it
        • delete node with children 1, replace with its child value then delete child
        • delete node with children 2, replace largest value from left subnodes or smallest value from right subnodes A tree having a right subtree with one value smaller than the root is shown to demonstrate that it is not a valid binary search tree
      • Breadth first search
        • level0, level1, level2(left to right), leve3(left to right)
      • Depth first search
        • In order traversal - left subtree, root, right subtree at each level)
        • Pre order traversal - root, left subtree and right subtree at each level
        • Post order traversal - left subtree, right subtree and root at each level
      • smallest value - left most
      • highest value - right most

Heap

  • Non Linear DS, must Complete binary tree (every level must be filled L & R, leaf node only lean towards left) and should satisfy heap
  • Binary heap
    • Min heap - every level root node is lesser than childs
      Min-heap
    • Max Heap - every level root node is greater than childs
      Max-heap
  • Binomial heap
  • Fibonaci heap
    Fibonacci Heap
  • Time Complexity:
    • Access Max / Min: O(1)
    • Insert: O(log(n))
    • Remove Max / Min: O(log(n))

Graph

  • A graph is Non Linear DS, a ordered pair of sets (V,E) vertices & edges
  • Tree has root node but graph no root node
  • Tree is only root to child. in graph any node to anynode possible
  • Ex: google maps, GPS, facebook, LinkedIn, e-commerce web sites
  • Graphs Direction Types
    • Undirected Graph - edges are bidirectional (adjacency relation is symmetric)
    • Directed Graph - edge are uni directional (adjacency relation is not symmetric)
    • Complete Graph - all nodes should have path
  • Graph Weight Types
    • Weighted Graph: a graph some value/cost
    • Unweighted Graph: a graph with no value/cost
  • Graph Cycle Types
    • Cyclic Graph - a graph has cycle
    • Acylic Graph - a graph which does have any cycle. tree is acyclic graph
  • Adjacent Nodes - if edge exists then called adjacent nodes
  • Graph Path - sequence of vertices connected by edges
    • Simple path - if all of its vertices are distinct
    • closed path - first and last node is same
    • Cycle - cycle is path, first & last node is same and all nodes to be distinct
  • Graph Connectivity
    • strongly connected - Directed & every node to node should have path
    • weekly connected - connected but Undirected
  • Degree of Node = number of edges its connected to it
    • InDegree - Incoming number of edges
    • OutDegree - outgoing number of edges
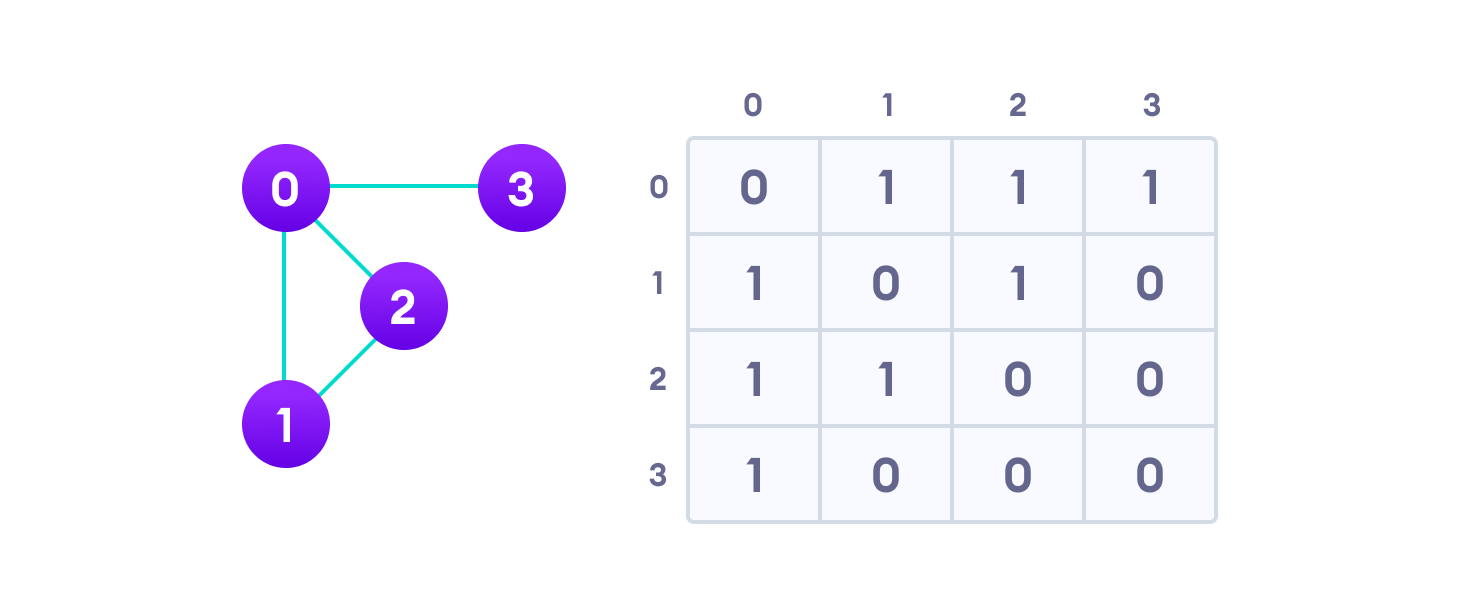
  • Adjaceny Matrix - matrix (0 or 1) representation b/n the nodes graph adjacency matrix for sample graph shows that the value of matrix element is 1 for the row and column that have an edge and 0 for row and column that don't have an edge
  • Adjacency List - array of linked lists representation of a nodes adjacency list representation represents graph as array of linked lists where index represents the vertex and each element in linked list represents the edges connected to that vertex
  • In Python use dictionaries

Search Algorithams

Linear Search Algorithm

  • Traverse array using for loop, if not march then -1
  • Time Complexity is O(n)

### Binary Search Algoritham - Array to be sorted - Find middle index & check the middle number, - if middle+1 < actual number, again middle index, etc


- Searching is based on n/2 iterations; - Iterative method - Recursive method - Ex: 10,14,19,26,27,31,33,35, 42, 44, 50 - Time Complexity is O(log n) ### Jump/block Search Algoritham - Like Linear Algorithms but - Typical time complexity O(√n). - Time Complexity is b/n (O(n)) and (O(log n))

Jump Search technique

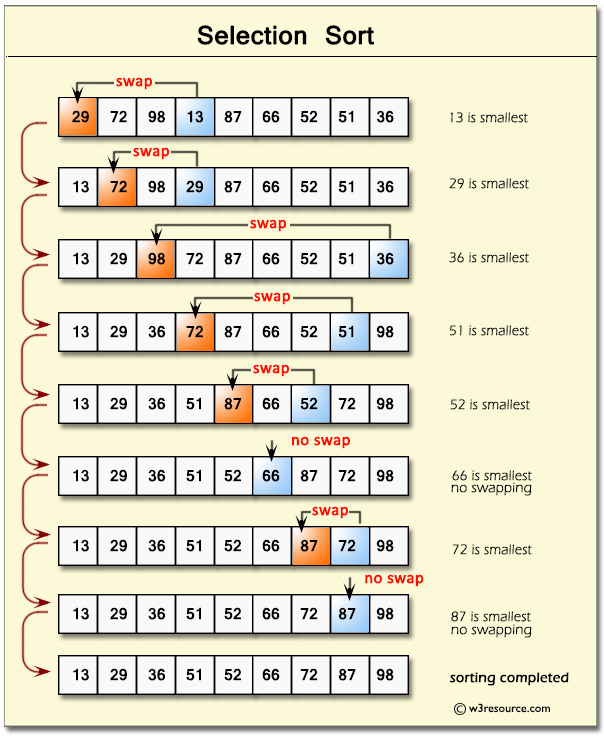
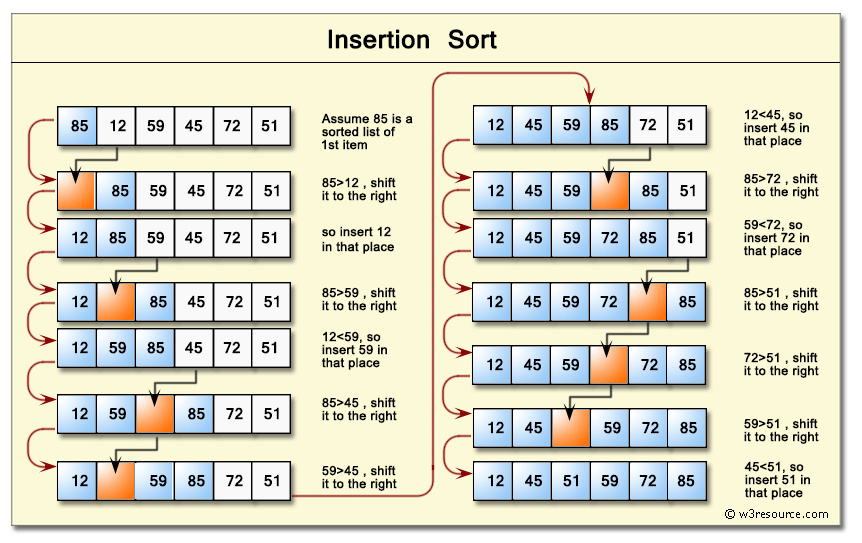
## Sort Algorithams

Bubble Sort Algorithm

  • Comparing adjacent items and swaps them untill intended order
  • The loop untill all are sorted
    • Time Complexity is O(n2)

### Quick Sort Algorithm - based on divide and conquer approach - choose pivot as last element - compare element with pivot, if greater than pivot, - swap small elements left => pivot element <= larger elements right - repeat the same untill single element - Time Complexity O(n2), best is O(n log n)

Quicksort Algorithm

### Selection Sort Algorithm * Step 1 − Set MIN to location 0 * Step 2 − Search the minimum element in the list * Step 3 − Swap with value at location MIN * Step 4 − Increment MIN to point to next element * Step 5 − Repeat until list is sorted - Time complexity is O(n2)

Python: Selection Sort

### Insertion Sort Algorithm - works like cards game sorting - take 2nd element as key, sort it with first - move it to next, compare with left sorted array - repeat - Time complexity is O(n2) best is O(n)

Python: Insertion sort

### Merge Sort Algorithm - based on Divide and Conquer Algorithm - divide array into 2 sub arrays untill single element - sort the left and right arrays - merge the smaller arrays into new array - Time complexity is O(n log n)

Merge Sort

### Shell Sort Algorithm - solve the problems of Insertion Sort Algorithm - split as sub array with perticular gap, sort sub arrays - move gap to diff position - reduce the gap size and repeat sorting of sub arrays - if gap size = 1 then apply insertion shot - Time complexity is O(n2), best is O(nlog n)

Shell Sort

## Problem Solviong Algorithms

Divide And Conquer

  • Problem will be divded in to sub problems
  • find solution for sub problem
  • combine all solutions to one soluiton
  • reucrisively solve
    • binary search
    • find min and max
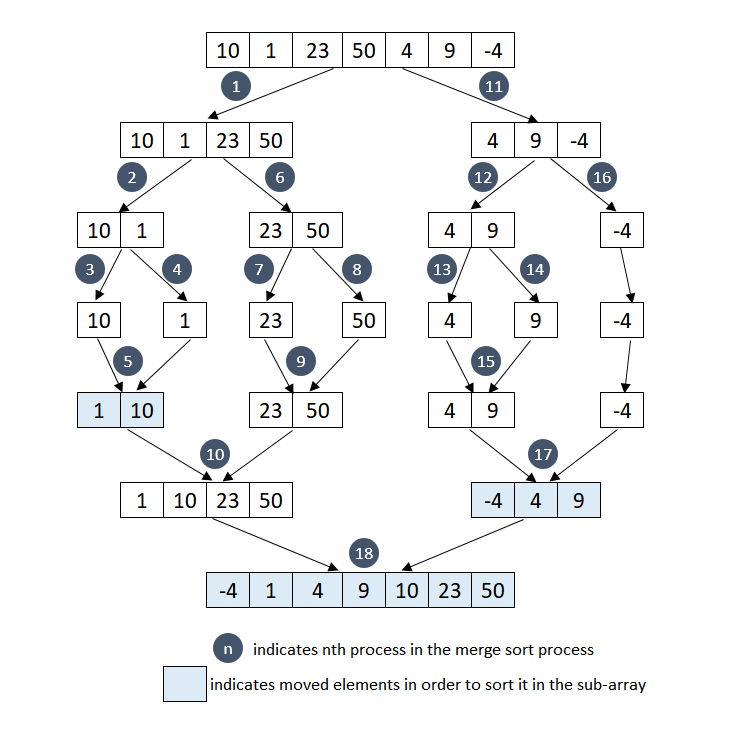
    • merge sort
    • quick sort
    • strassens matrix multiplication

Backtracking Algorithm/Brute force approach

  • Tries all the possibilities, chooses the desired/best solutions

  • Good Practice to come up with solution to all possible

  • least efficient but guaranteed a solution

  • Backtracking aproach

    • find all the possible ways

  • State space tree

    • define level by level

Greedy algorithm

  • top-down approach
    • Greedy Choice Property
      • choosing the best choice at each step
      • most obvious and immediate benefit
      top-down approach for fibonacci series in dynamic programming
    • Optimal Substructure
      • solution to its subproblems so that problem can be solved
      • Optimal substructure - Wikipedia

Branching and bound Algorithms

Dijkstra's Algorithm

Dynamic Programming

  • technique to efficiently solve a class of problems that have overlapping subproblems
  • problem can be divided into smaller subproblems
  • if overlapping among subproblems, solution will be saved for future reference Ex: 0,1,1,2,3,5,8,13,21,34,55...(n-1 + n-2)

Backtracking Algorithm

Links