|
| 1 | +--- |
| 2 | +Title: "Student's t Distribution" |
| 3 | +Description: "Explains the Student's t distribution used in statistical inference when sample sizes are small or population standard deviation is unknown." |
| 4 | +Subjects: |
| 5 | + - 'Computer Science' |
| 6 | + - 'Data Science' |
| 7 | +Tags: |
| 8 | + - 'Data Distributions' |
| 9 | + - 'Probability' |
| 10 | + - 'Python' |
| 11 | + - 'Statistics' |
| 12 | +CatalogContent: |
| 13 | + - 'learn-python-3' |
| 14 | + - 'paths/data-science' |
| 15 | +--- |
| 16 | + |
| 17 | +The **Student's t distribution** is a probability distribution used in statistical inference when working with small sample sizes or when the population standard deviation is unknown. It resembles the normal distribution but features heavier tails, making it more appropriate for estimating population parameters with limited data. This distribution is fundamental in hypothesis testing, confidence interval construction, and statistical modeling. |
| 18 | + |
| 19 | +The formula for a t-statistic is given by: |
| 20 | + |
| 21 | +$$t = \frac{\bar{x} - \mu}{s / \sqrt{n}}$$ |
| 22 | + |
| 23 | +Where: |
| 24 | + |
| 25 | +- `t`: t-statistic value |
| 26 | +- $\bar{x}$: sample mean |
| 27 | +- `μ`: population mean |
| 28 | +- `s`: sample standard deviation |
| 29 | +- `n`: sample size |
| 30 | + |
| 31 | +The probability density function (PDF) of the t-distribution with v degrees of freedom is: |
| 32 | + |
| 33 | +$$f(t) = \frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\Gamma(\frac{v}{2})} (1 + \frac{t^2}{v})^{-\frac{v+1}{2}}$$ |
| 34 | + |
| 35 | +Where: |
| 36 | + |
| 37 | +- `Γ` is the gamma function |
| 38 | +- `v` represents the degrees of freedom (df = n-1) |
| 39 | + |
| 40 | +## Key Properties |
| 41 | + |
| 42 | +The t-distribution has several distinctive characteristics: |
| 43 | + |
| 44 | +1. **Degrees of Freedom**: Calculated as `n-1` (sample size minus one), this parameter determines the shape of the distribution. |
| 45 | +2. **Symmetry**: Like the normal distribution, the t-distribution is symmetric around zero. |
| 46 | +3. **Heavier Tails**: Compared to the normal distribution, the t-distribution has heavier tails, meaning extreme values are more probable. |
| 47 | +4. **Convergence to Normal Distribution**: As degrees of freedom increase, the t-distribution approaches the standard normal distribution. When df > 30, the t-distribution is practically indistinguishable from the normal distribution. |
| 48 | +5. **Mean, Median, and Mode**: All equal to 0 when degrees of freedom > 1. |
| 49 | +6. **Variance**: Equal to `v/(v-2)` for v > 2, undefined for 1 < v ≤ 2, and infinite for v = 1. |
| 50 | + |
| 51 | +> **Note:** The heavier tails of the t-distribution account for the additional uncertainty introduced when estimating the population standard deviation from a sample. |
| 52 | +
|
| 53 | +## Applications |
| 54 | + |
| 55 | +The Student's t distribution is widely used in various statistical scenarios: |
| 56 | + |
| 57 | +1. **Hypothesis Testing**: In t-tests to determine if there's a significant difference between sample means and population means, or between two sample means when sample sizes are small (n<30) or population standard deviation is unknown. |
| 58 | +2. **Confidence Intervals**: To establish intervals for population parameters when the population standard deviation is unknown or sample sizes are small (n<30). |
| 59 | +3. **Regression Analysis**: In determining the significance of regression coefficients. |
| 60 | + |
| 61 | +## Example: Plotting a t-Distribution in Python |
| 62 | + |
| 63 | +This example demonstrates how to generate and visualize a Student's t-distribution for different degrees of freedom (df): |
| 64 | + |
| 65 | +```py |
| 66 | +import numpy as np |
| 67 | +import matplotlib.pyplot as plt |
| 68 | +from scipy.stats import t |
| 69 | + |
| 70 | +# Define x values |
| 71 | +x = np.linspace(-4, 4, 1000) |
| 72 | + |
| 73 | +# Plot t-distributions for different degrees of freedom |
| 74 | +dfs = [1, 5, 10, 30] # Different sample sizes |
| 75 | +for df in dfs: |
| 76 | + plt.plot(x, t.pdf(x, df), label=f'df = {df}') |
| 77 | + |
| 78 | +# Plot standard normal distribution for comparison |
| 79 | +from scipy.stats import norm |
| 80 | +plt.plot(x, norm.pdf(x), 'k--', label='Normal (df → ∞)') |
| 81 | + |
| 82 | +# Labels and legend |
| 83 | +plt.title("Student's t-Distribution for Different Degrees of Freedom") |
| 84 | +plt.xlabel("t value") |
| 85 | +plt.ylabel("Probability Density") |
| 86 | +plt.legend() |
| 87 | +plt.grid() |
| 88 | + |
| 89 | +# Show plot |
| 90 | +plt.show() |
| 91 | +``` |
| 92 | + |
| 93 | +This example results in the following output: |
| 94 | + |
| 95 | +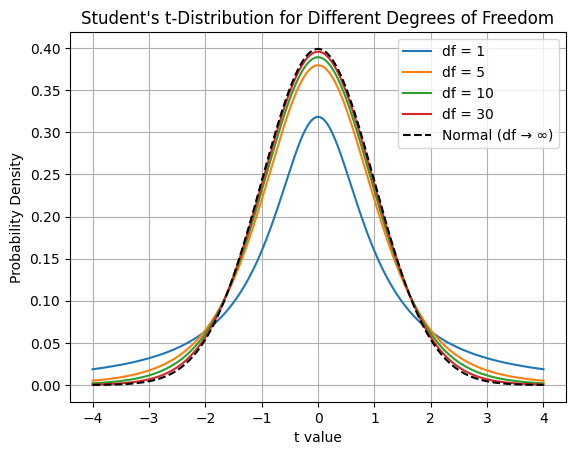 |
| 96 | + |
| 97 | +For a comprehensive understanding of statistical distributions and their applications, consider exploring Codecademy's [Master Statistics with Python](https://www.codecademy.com/learn/paths/master-statistics-with-python) skill path. |
0 commit comments