|
| 1 | +#### 1465. 切割后面积最大的蛋糕 |
| 2 | + |
| 3 | +难度:中等 |
| 4 | + |
| 5 | +--- |
| 6 | + |
| 7 | +矩形蛋糕的高度为 `h` 且宽度为 `w`,给你两个整数数组 `horizontalCuts` 和 `verticalCuts`,其中: |
| 8 | + |
| 9 | +* `horizontalCuts[i]` 是从矩形蛋糕顶部到第 `i` 个水平切口的距离 |
| 10 | +* `verticalCuts[j]` 是从矩形蛋糕的左侧到第 `j` 个竖直切口的距离 |
| 11 | + |
| 12 | +请你按数组 _`horizontalCuts`_ 和 _`verticalCuts`_ 中提供的水平和竖直位置切割后,请你找出 **面积最大** 的那份蛋糕,并返回其 **面积** 。由于答案可能是一个很大的数字,因此需要将结果 **对** `10^9 + 7` **取余** 后返回。 |
| 13 | + |
| 14 | + **示例 1:** |
| 15 | + |
| 16 | +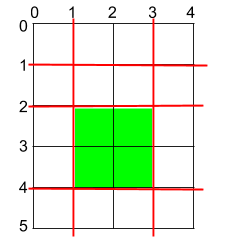 |
| 17 | + |
| 18 | +``` |
| 19 | +输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] |
| 20 | +输出:4 |
| 21 | +解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。 |
| 22 | +``` |
| 23 | + |
| 24 | + **示例 2:** |
| 25 | + |
| 26 | + **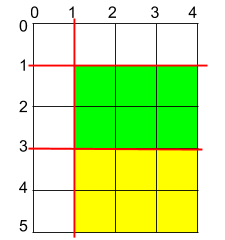** |
| 27 | + |
| 28 | +``` |
| 29 | +输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] |
| 30 | +输出:6 |
| 31 | +解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。 |
| 32 | +``` |
| 33 | + |
| 34 | + **示例 3:** |
| 35 | + |
| 36 | +``` |
| 37 | +输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] |
| 38 | +输出:9 |
| 39 | +``` |
| 40 | + |
| 41 | + **提示:** |
| 42 | + |
| 43 | +* `2 <= h, w <= 10^9` |
| 44 | +* `1 <= horizontalCuts.length <= min(h - 1, 10^5)` |
| 45 | +* `1 <= verticalCuts.length <= min(w - 1, 10^5)` |
| 46 | +* `1 <= horizontalCuts[i] < h` |
| 47 | +* `1 <= verticalCuts[i] < w` |
| 48 | +* 题目数据保证 `horizontalCuts` 中的所有元素各不相同 |
| 49 | +* 题目数据保证 `verticalCuts` 中的所有元素各不相同 |
| 50 | + |
| 51 | +--- |
| 52 | + |
| 53 | +贪心: |
| 54 | + |
| 55 | +取横轴和纵轴的最大值并相乘即可,注意相乘后的结果可能越界,所以先转换为 `long` 类型再取余。 |
| 56 | + |
| 57 | +```Java |
| 58 | +class Solution { |
| 59 | + public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) { |
| 60 | + Arrays.sort(horizontalCuts); |
| 61 | + Arrays.sort(verticalCuts); |
| 62 | + return (int) ((long) calculate(horizontalCuts, h) * calculate(verticalCuts, w) % 1000000007); |
| 63 | + } |
| 64 | + |
| 65 | + private int calculate(int[] cuts, int length){ |
| 66 | + int pre = 0, res = 0; |
| 67 | + for(int cut: cuts){ |
| 68 | + res = Math.max(res, cut - pre); |
| 69 | + pre = cut; |
| 70 | + } |
| 71 | + return Math.max(res, length - pre); |
| 72 | + } |
| 73 | +} |
| 74 | +``` |
0 commit comments