|
| 1 | +# [304. Range Sum Query 2D - Immutable](https://leetcode.com/problems/range-sum-query-2d-immutable/) |
| 2 | + |
| 3 | + |
| 4 | +## 题目 |
| 5 | + |
| 6 | +Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2). |
| 7 | + |
| 8 | + |
| 9 | + |
| 10 | +The above rectangle (with the red border) is defined by (row1, col1) = **(2, 1)** and (row2, col2) = **(4, 3)**, which contains sum = **8**. |
| 11 | + |
| 12 | +**Example:** |
| 13 | + |
| 14 | +``` |
| 15 | +Given matrix = [ |
| 16 | + [3, 0, 1, 4, 2], |
| 17 | + [5, 6, 3, 2, 1], |
| 18 | + [1, 2, 0, 1, 5], |
| 19 | + [4, 1, 0, 1, 7], |
| 20 | + [1, 0, 3, 0, 5] |
| 21 | +] |
| 22 | +
|
| 23 | +sumRegion(2, 1, 4, 3) -> 8 |
| 24 | +sumRegion(1, 1, 2, 2) -> 11 |
| 25 | +sumRegion(1, 2, 2, 4) -> 12 |
| 26 | +
|
| 27 | +``` |
| 28 | + |
| 29 | +**Note:** |
| 30 | + |
| 31 | +1. You may assume that the matrix does not change. |
| 32 | +2. There are many calls to sumRegion function. |
| 33 | +3. You may assume that row1 ≤ row2 and col1 ≤ col2. |
| 34 | + |
| 35 | +## 题目大意 |
| 36 | + |
| 37 | +给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。 |
| 38 | + |
| 39 | +## 解题思路 |
| 40 | + |
| 41 | +- 这一题是一维数组前缀和的进阶版本。定义 f(x,y) 代表矩形左上角 (0,0),右下角 (x,y) 内的元素和。{{< katex display >}} f(i,j) = \sum_{x=0}^{i}\sum_{y=0}^{j} Matrix[x][y]{{< /katex >}} |
| 42 | + |
| 43 | + {{< katex display >}} |
| 44 | + \begin{aligned} |
| 45 | + f(i,j) &= \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j] + \sum_{y=0}^{j-1} Matrix[i][y] + Matrix[i][j]\\ |
| 46 | + &= (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j]) + (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{y=0}^{j-1} Matrix[i][y]) - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\ |
| 47 | + &= \sum_{x=0}^{i-1}\sum_{y=0}^{j} Matrix[x][y] + \sum_{x=0}^{i}\sum_{y=0}^{j-1} Matrix[x][y] - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\ |
| 48 | + &= f(i-1,j) + f(i,j-1) - f(i-1,j-1) + Matrix[i][j] |
| 49 | + \end{aligned} |
| 50 | + {{< /katex >}} |
| 51 | + |
| 52 | +- 于是得到递推的关系式:`f(i, j) = f(i-1, j) + f(i, j-1) - f(i-1, j-1) + matrix[i][j]`,写代码为了方便,新建一个 `m+1 * n+1` 的矩阵,这样就不需要对 `row = 0` 和 `col = 0` 做单独处理了。上述推导公式如果画成图也很好理解: |
| 53 | + |
| 54 | + 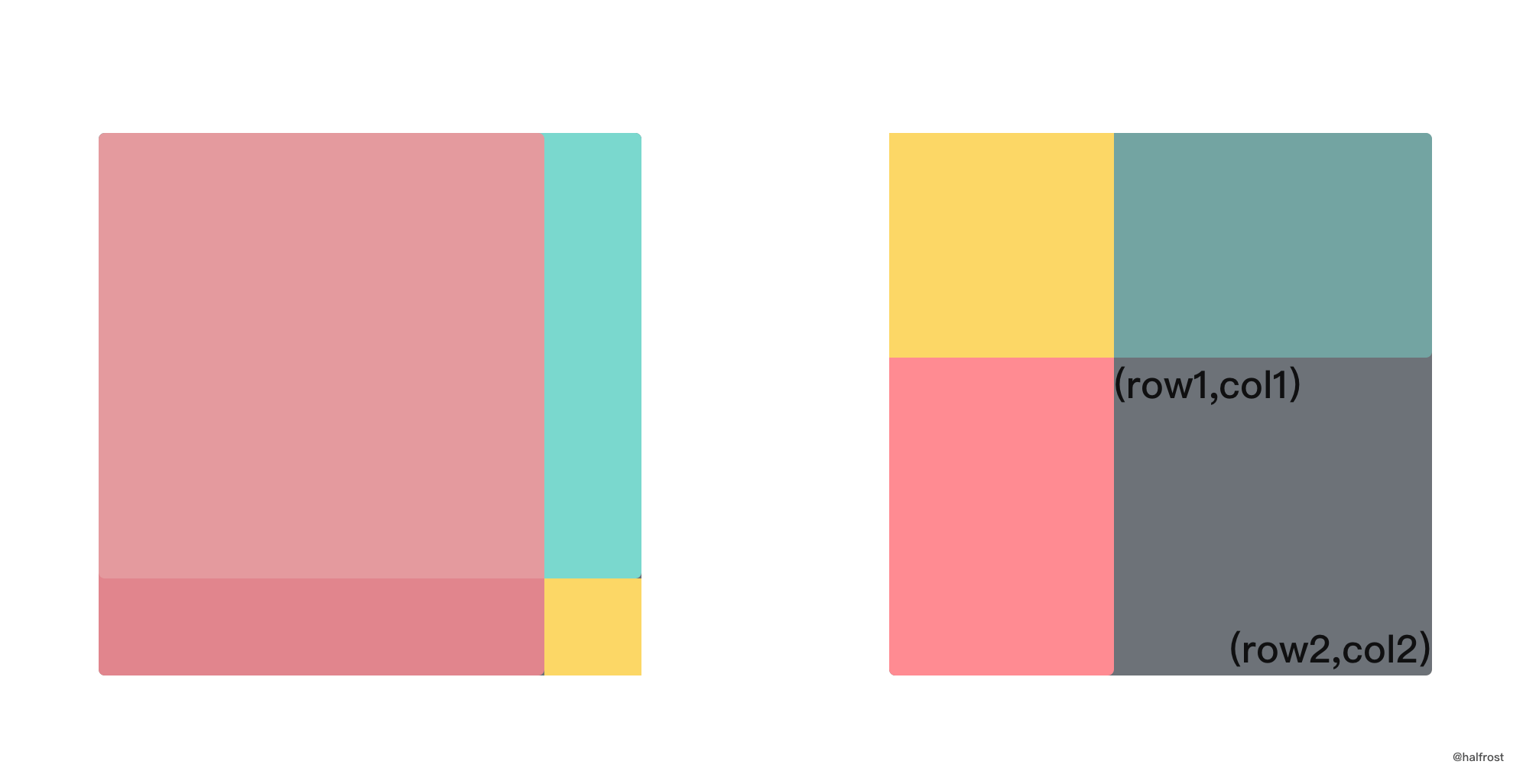 |
| 55 | + |
| 56 | + 左图中大的矩形由粉红色的矩形 + 绿色矩形 - 粉红色和绿色重叠部分 + 黄色部分。这就对应的是上面推导出来的递推公式。左图是矩形左上角为 (0,0) 的情况,更加一般的情况是右图,左上角是任意的坐标,公式不变。 |
| 57 | + |
| 58 | +- 时间复杂度:初始化 O(mn),查询 O(1)。空间复杂度 O(mn) |
| 59 | + |
| 60 | +## 代码 |
| 61 | + |
| 62 | +```go |
| 63 | +package leetcode |
| 64 | + |
| 65 | +type NumMatrix struct { |
| 66 | + cumsum [][]int |
| 67 | +} |
| 68 | + |
| 69 | +func Constructor(matrix [][]int) NumMatrix { |
| 70 | + if len(matrix) == 0 { |
| 71 | + return NumMatrix{nil} |
| 72 | + } |
| 73 | + cumsum := make([][]int, len(matrix)+1) |
| 74 | + cumsum[0] = make([]int, len(matrix[0])+1) |
| 75 | + for i := range matrix { |
| 76 | + cumsum[i+1] = make([]int, len(matrix[i])+1) |
| 77 | + for j := range matrix[i] { |
| 78 | + cumsum[i+1][j+1] = matrix[i][j] + cumsum[i][j+1] + cumsum[i+1][j] - cumsum[i][j] |
| 79 | + } |
| 80 | + } |
| 81 | + return NumMatrix{cumsum} |
| 82 | +} |
| 83 | + |
| 84 | +func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int { |
| 85 | + cumsum := this.cumsum |
| 86 | + return cumsum[row2+1][col2+1] - cumsum[row1][col2+1] - cumsum[row2+1][col1] + cumsum[row1][col1] |
| 87 | +} |
| 88 | + |
| 89 | +/** |
| 90 | + * Your NumMatrix object will be instantiated and called as such: |
| 91 | + * obj := Constructor(matrix); |
| 92 | + * param_1 := obj.SumRegion(row1,col1,row2,col2); |
| 93 | + */ |
| 94 | +``` |
| 95 | + |
| 96 | + |
| 97 | +---------------------------------------------- |
| 98 | +<div style="display: flex;justify-content: space-between;align-items: center;"> |
| 99 | +<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0300~0399/0303.Range-Sum-Query-Immutable/">⬅️上一页</a></p> |
| 100 | +<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0300~0399/0306.Additive-Number/">下一页➡️</a></p> |
| 101 | +</div> |
0 commit comments