|
| 1 | +3419\. Minimize the Maximum Edge Weight of Graph |
| 2 | + |
| 3 | +Medium |
| 4 | + |
| 5 | +You are given two integers, `n` and `threshold`, as well as a **directed** weighted graph of `n` nodes numbered from 0 to `n - 1`. The graph is represented by a **2D** integer array `edges`, where <code>edges[i] = [A<sub>i</sub>, B<sub>i</sub>, W<sub>i</sub>]</code> indicates that there is an edge going from node <code>A<sub>i</sub></code> to node <code>B<sub>i</sub></code> with weight <code>W<sub>i</sub></code>. |
| 6 | + |
| 7 | +You have to remove some edges from this graph (possibly **none**), so that it satisfies the following conditions: |
| 8 | + |
| 9 | +* Node 0 must be reachable from all other nodes. |
| 10 | +* The **maximum** edge weight in the resulting graph is **minimized**. |
| 11 | +* Each node has **at most** `threshold` outgoing edges. |
| 12 | + |
| 13 | +Return the **minimum** possible value of the **maximum** edge weight after removing the necessary edges. If it is impossible for all conditions to be satisfied, return -1. |
| 14 | + |
| 15 | +**Example 1:** |
| 16 | + |
| 17 | +**Input:** n = 5, edges = [[1,0,1],[2,0,2],[3,0,1],[4,3,1],[2,1,1]], threshold = 2 |
| 18 | + |
| 19 | +**Output:** 1 |
| 20 | + |
| 21 | +**Explanation:** |
| 22 | + |
| 23 | +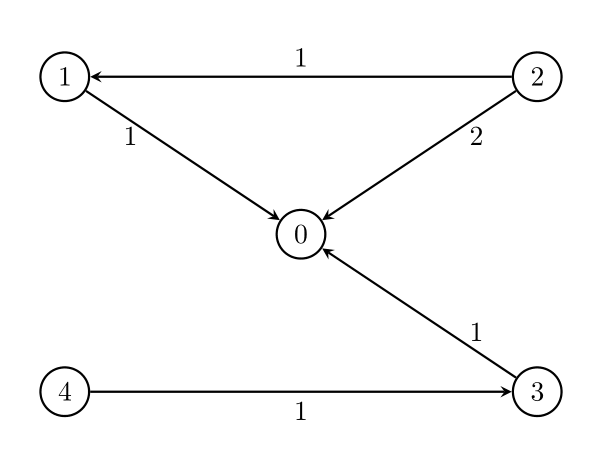 |
| 24 | + |
| 25 | +Remove the edge `2 -> 0`. The maximum weight among the remaining edges is 1. |
| 26 | + |
| 27 | +**Example 2:** |
| 28 | + |
| 29 | +**Input:** n = 5, edges = [[0,1,1],[0,2,2],[0,3,1],[0,4,1],[1,2,1],[1,4,1]], threshold = 1 |
| 30 | + |
| 31 | +**Output:** \-1 |
| 32 | + |
| 33 | +**Explanation:** |
| 34 | + |
| 35 | +It is impossible to reach node 0 from node 2. |
| 36 | + |
| 37 | +**Example 3:** |
| 38 | + |
| 39 | +**Input:** n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[3,4,2],[4,0,1]], threshold = 1 |
| 40 | + |
| 41 | +**Output:** 2 |
| 42 | + |
| 43 | +**Explanation:** |
| 44 | + |
| 45 | +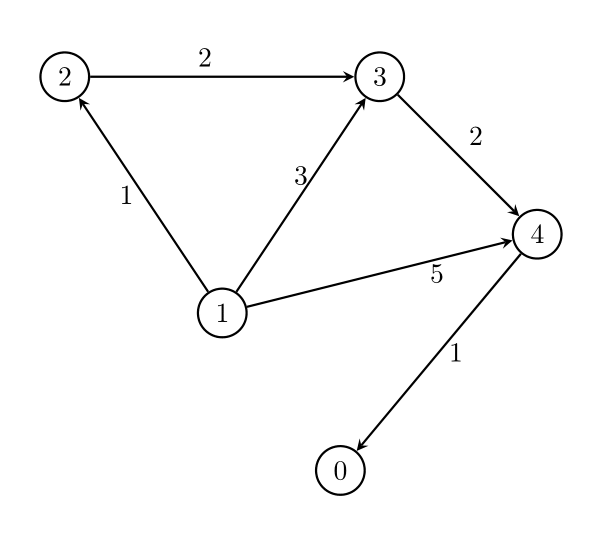 |
| 46 | + |
| 47 | +Remove the edges `1 -> 3` and `1 -> 4`. The maximum weight among the remaining edges is 2. |
| 48 | + |
| 49 | +**Example 4:** |
| 50 | + |
| 51 | +**Input:** n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[4,0,1]], threshold = 1 |
| 52 | + |
| 53 | +**Output:** \-1 |
| 54 | + |
| 55 | +**Constraints:** |
| 56 | + |
| 57 | +* <code>2 <= n <= 10<sup>5</sup></code> |
| 58 | +* `1 <= threshold <= n - 1` |
| 59 | +* <code>1 <= edges.length <= min(10<sup>5</sup>, n * (n - 1) / 2).</code> |
| 60 | +* `edges[i].length == 3` |
| 61 | +* <code>0 <= A<sub>i</sub>, B<sub>i</sub> < n</code> |
| 62 | +* <code>A<sub>i</sub> != B<sub>i</sub></code> |
| 63 | +* <code>1 <= W<sub>i</sub> <= 10<sup>6</sup></code> |
| 64 | +* There **may be** multiple edges between a pair of nodes, but they must have unique weights. |
0 commit comments