-
Notifications
You must be signed in to change notification settings - Fork 1
Added tasks 3070-3081 #1
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Changes from all commits
File filter
Filter by extension
Conversations
Jump to
Diff view
Diff view
There are no files selected for viewing
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,24 @@ | ||
| package g3001_3100.s3070_count_submatrices_with_top_left_element_and_sum_less_than_k | ||
|
|
||
| // #Medium #Array #Matrix #Prefix_Sum #2024_04_16_Time_773_ms_(85.71%)_Space_134.2_MB_(71.43%) | ||
|
|
||
| class Solution { | ||
| fun countSubmatrices(grid: Array<IntArray>, k: Int): Int { | ||
| val n = grid[0].size | ||
| val sums = IntArray(n) | ||
| var ans = 0 | ||
| for (ints in grid) { | ||
| var sum = 0 | ||
| for (col in 0 until n) { | ||
| sum += ints[col] | ||
| sums[col] += sum | ||
| if (sums[col] <= k) { | ||
| ans++ | ||
| } else { | ||
| break | ||
| } | ||
| } | ||
| } | ||
| return ans | ||
| } | ||
| } |
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,35 @@ | ||
| 3070\. Count Submatrices with Top-Left Element and Sum Less Than k | ||
|
|
||
| Medium | ||
|
|
||
| You are given a **0-indexed** integer matrix `grid` and an integer `k`. | ||
|
|
||
| Return _the **number** of submatrices that contain the top-left element of the_ `grid`, _and have a sum less than or equal to_ `k`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| 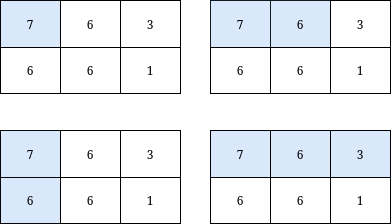 | ||
|
|
||
| **Input:** grid = [[7,6,3],[6,6,1]], k = 18 | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** There are only 4 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 18. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 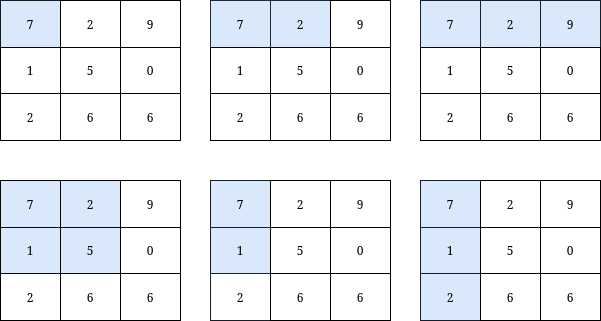 | ||
|
There was a problem hiding this comment. Choose a reason for hiding this commentThe reason will be displayed to describe this comment to others. Learn more. This image is missing a text alternative. This is a problem for people using screen readers. |
||
|
|
||
| **Input:** grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20 | ||
|
|
||
| **Output:** 6 | ||
|
|
||
| **Explanation:** There are only 6 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 20. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `m == grid.length` | ||
| * `n == grid[i].length` | ||
| * `1 <= n, m <= 1000` | ||
| * `0 <= grid[i][j] <= 1000` | ||
| * <code>1 <= k <= 10<sup>9</sup></code> | ||
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,50 @@ | ||
| package g3001_3100.s3071_minimum_operations_to_write_the_letter_y_on_a_grid | ||
|
|
||
| // #Medium #Array #Hash_Table #Matrix #Counting | ||
| // #2024_04_16_Time_268_ms_(91.11%)_Space_42.6_MB_(93.33%) | ||
|
|
||
| import kotlin.math.min | ||
|
|
||
| class Solution { | ||
| fun minimumOperationsToWriteY(arr: Array<IntArray>): Int { | ||
| val n = arr.size | ||
| val cnt1 = IntArray(3) | ||
| val cnt2 = IntArray(3) | ||
| val x = n / 2 | ||
| val y = n / 2 | ||
| for (j in x until n) { | ||
| cnt1[arr[j][y]]++ | ||
| arr[j][y] = 3 | ||
| } | ||
| for (j in x downTo 0) { | ||
| if (arr[j][j] != 3) { | ||
| cnt1[arr[j][j]]++ | ||
| } | ||
| arr[j][j] = 3 | ||
| } | ||
| for (j in x downTo 0) { | ||
| if (arr[j][n - 1 - j] != 3) { | ||
| cnt1[arr[j][n - 1 - j]]++ | ||
| } | ||
| arr[j][n - 1 - j] = 3 | ||
| } | ||
| for (ints in arr) { | ||
| for (j in 0 until n) { | ||
| if (ints[j] != 3) { | ||
| cnt2[ints[j]]++ | ||
| } | ||
| } | ||
| } | ||
| val s1 = cnt1[0] + cnt1[1] + cnt1[2] | ||
| val s2 = cnt2[0] + cnt2[1] + cnt2[2] | ||
| var min = Int.MAX_VALUE | ||
| for (i in 0..2) { | ||
| for (j in 0..2) { | ||
| if (i != j) { | ||
| min = min((s1 - cnt1[i] + s2 - cnt2[j]), min) | ||
| } | ||
| } | ||
| } | ||
| return min | ||
| } | ||
| } |
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,46 @@ | ||
| 3071\. Minimum Operations to Write the Letter Y on a Grid | ||
|
|
||
| Medium | ||
|
|
||
| You are given a **0-indexed** `n x n` grid where `n` is odd, and `grid[r][c]` is `0`, `1`, or `2`. | ||
|
|
||
| We say that a cell belongs to the Letter **Y** if it belongs to one of the following: | ||
|
|
||
| * The diagonal starting at the top-left cell and ending at the center cell of the grid. | ||
| * The diagonal starting at the top-right cell and ending at the center cell of the grid. | ||
| * The vertical line starting at the center cell and ending at the bottom border of the grid. | ||
|
|
||
| The Letter **Y** is written on the grid if and only if: | ||
|
|
||
| * All values at cells belonging to the Y are equal. | ||
| * All values at cells not belonging to the Y are equal. | ||
| * The values at cells belonging to the Y are different from the values at cells not belonging to the Y. | ||
|
|
||
| Return _the **minimum** number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to_ `0`_,_ `1`_,_ _or_ `2`_._ | ||
|
|
||
| **Example 1:** | ||
|
|
||
| 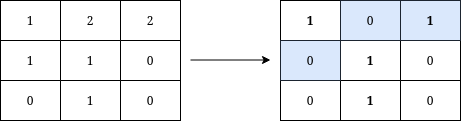 | ||
|
There was a problem hiding this comment. Choose a reason for hiding this commentThe reason will be displayed to describe this comment to others. Learn more. This image is missing a text alternative. This is a problem for people using screen readers. |
||
|
|
||
| **Input:** grid = [[1,2,2],[1,1,0],[0,1,0]] | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0. It can be shown that 3 is the minimum number of operations needed to write Y on the grid. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 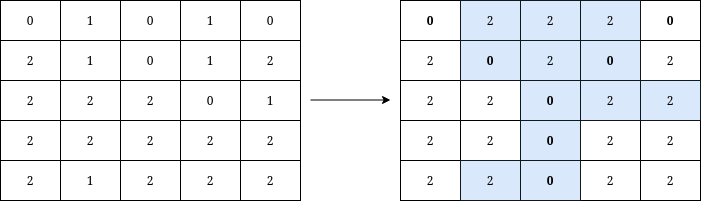 | ||
|
There was a problem hiding this comment. Choose a reason for hiding this commentThe reason will be displayed to describe this comment to others. Learn more. This image is missing a text alternative. This is a problem for people using screen readers. |
||
|
|
||
| **Input:** grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]] | ||
|
|
||
| **Output:** 12 | ||
|
|
||
| **Explanation:** We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. It can be shown that 12 is the minimum number of operations needed to write Y on the grid. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `3 <= n <= 49` | ||
| * `n == grid.length == grid[i].length` | ||
| * `0 <= grid[i][j] <= 2` | ||
| * `n` is odd. | ||
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,94 @@ | ||
| package g3001_3100.s3072_distribute_elements_into_two_arrays_ii | ||
|
|
||
| // #Hard #Array #Simulation #Segment_Tree #Binary_Indexed_Tree | ||
| // #2024_04_16_Time_890_ms_(100.00%)_Space_77.6_MB_(54.17%) | ||
|
|
||
| @Suppress("NAME_SHADOWING") | ||
| class Solution { | ||
| internal inner class BIT(size: Int) { | ||
| private val tree = IntArray(size + 1) | ||
|
|
||
| fun update(ind: Int) { | ||
| var ind = ind | ||
| while (ind < tree.size) { | ||
| tree[ind]++ | ||
| ind += lsb(ind) | ||
| } | ||
| } | ||
|
|
||
| fun rsq(ind: Int): Int { | ||
| var ind = ind | ||
| var sum = 0 | ||
| while (ind > 0) { | ||
| sum += tree[ind] | ||
| ind -= lsb(ind) | ||
| } | ||
| return sum | ||
| } | ||
|
|
||
| private fun lsb(n: Int): Int { | ||
| return n and (-n) | ||
| } | ||
| } | ||
|
|
||
| fun resultArray(source: IntArray): IntArray { | ||
| val nums = shrink(source) | ||
| val arr1 = IntArray(nums.size) | ||
| val arr2 = IntArray(nums.size) | ||
| arr1[0] = source[0] | ||
| arr2[0] = source[1] | ||
| var p1 = 0 | ||
| var p2 = 0 | ||
| val bit1 = BIT(nums.size) | ||
| bit1.update(nums[0]) | ||
| val bit2 = BIT(nums.size) | ||
| bit2.update(nums[1]) | ||
| for (i in 2 until nums.size) { | ||
| val g1 = p1 + 1 - bit1.rsq(nums[i]) | ||
| val g2 = p2 + 1 - bit2.rsq(nums[i]) | ||
| if (g1 > g2) { | ||
| p1++ | ||
| arr1[p1] = source[i] | ||
| bit1.update(nums[i]) | ||
| } else if (g1 < g2) { | ||
| p2++ | ||
| arr2[p2] = source[i] | ||
| bit2.update(nums[i]) | ||
| } else if (p1 < p2) { | ||
| p1++ | ||
| arr1[p1] = source[i] | ||
| bit1.update(nums[i]) | ||
| } else if (p1 > p2) { | ||
| p2++ | ||
| arr2[p2] = source[i] | ||
| bit2.update(nums[i]) | ||
| } else { | ||
| p1++ | ||
| arr1[p1] = source[i] | ||
| bit1.update(nums[i]) | ||
| } | ||
| } | ||
| for (i in p1 + 1 until arr1.size) { | ||
| arr1[i] = arr2[i - p1 - 1] | ||
| } | ||
|
|
||
| return arr1 | ||
| } | ||
|
|
||
| private fun shrink(nums: IntArray): IntArray { | ||
| val b = LongArray(nums.size) | ||
| for (i in nums.indices) { | ||
| b[i] = nums[i].toLong() shl 32 or i.toLong() | ||
| } | ||
| b.sort() | ||
| val result = IntArray(nums.size) | ||
| var p = 1 | ||
| for (i in nums.indices) { | ||
| if (i > 0 && (b[i] xor b[i - 1]) shr 32 != 0L) { | ||
| p++ | ||
| } | ||
| result[b[i].toInt()] = p | ||
| } | ||
| return result | ||
| } | ||
| } |
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,59 @@ | ||
| 3072\. Distribute Elements Into Two Arrays II | ||
|
|
||
| Hard | ||
|
|
||
| You are given a **1-indexed** array of integers `nums` of length `n`. | ||
|
|
||
| We define a function `greaterCount` such that `greaterCount(arr, val)` returns the number of elements in `arr` that are **strictly greater** than `val`. | ||
|
|
||
| You need to distribute all the elements of `nums` between two arrays `arr1` and `arr2` using `n` operations. In the first operation, append `nums[1]` to `arr1`. In the second operation, append `nums[2]` to `arr2`. Afterwards, in the <code>i<sup>th</sup></code> operation: | ||
|
|
||
| * If `greaterCount(arr1, nums[i]) > greaterCount(arr2, nums[i])`, append `nums[i]` to `arr1`. | ||
| * If `greaterCount(arr1, nums[i]) < greaterCount(arr2, nums[i])`, append `nums[i]` to `arr2`. | ||
| * If `greaterCount(arr1, nums[i]) == greaterCount(arr2, nums[i])`, append `nums[i]` to the array with a **lesser** number of elements. | ||
| * If there is still a tie, append `nums[i]` to `arr1`. | ||
|
|
||
| The array `result` is formed by concatenating the arrays `arr1` and `arr2`. For example, if `arr1 == [1,2,3]` and `arr2 == [4,5,6]`, then `result = [1,2,3,4,5,6]`. | ||
|
|
||
| Return _the integer array_ `result`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [2,1,3,3] | ||
|
|
||
| **Output:** [2,3,1,3] | ||
|
|
||
| **Explanation:** After the first 2 operations, arr1 = [2] and arr2 = [1]. | ||
|
|
||
| In the 3<sup>rd</sup> operation, the number of elements greater than 3 is zero in both arrays. | ||
|
|
||
| Also, the lengths are equal, hence, append nums[3] to arr1. In the 4<sup>th</sup> operation, the number of elements greater than 3 is zero in both arrays. As the length of arr2 is lesser, hence, append nums[4] to arr2. | ||
|
|
||
| After 4 operations, arr1 = [2,3] and arr2 = [1,3]. Hence, the array result formed by concatenation is [2,3,1,3]. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [5,14,3,1,2] | ||
|
|
||
| **Output:** [5,3,1,2,14] | ||
|
|
||
| **Explanation:** After the first 2 operations, arr1 = [5] and arr2 = [14]. | ||
|
|
||
| In the 3<sup>rd</sup> operation, the number of elements greater than 3 is one in both arrays. Also, the lengths are equal, hence, append nums[3] to arr1. | ||
|
|
||
| In the 4<sup>th</sup> operation, the number of elements greater than 1 is greater in arr1 than arr2 (2 > 1). Hence, append nums[4] to arr1. In the 5<sup>th</sup> operation, the number of elements greater than 2 is greater in arr1 than arr2 (2 > 1). Hence, append nums[5] to arr1. | ||
|
|
||
| zAfter 5 operations, arr1 = [5,3,1,2] and arr2 = [14]. Hence, the array result formed by concatenation is [5,3,1,2,14]. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** nums = [3,3,3,3] | ||
|
|
||
| **Output:** [3,3,3,3] | ||
|
|
||
| **Explanation:** At the end of 4 operations, arr1 = [3,3] and arr2 = [3,3]. Hence, the array result formed by concatenation is [3,3,3,3]. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>3 <= n <= 10<sup>5</sup></code> | ||
| * <code>1 <= nums[i] <= 10<sup>9</sup></code> |
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,34 @@ | ||
| package g3001_3100.s3074_apple_redistribution_into_boxes | ||
|
|
||
| // #Easy #Array #Sorting #Greedy #2024_04_16_Time_168_ms_(97.37%)_Space_35.4_MB_(100.00%) | ||
|
|
||
| import kotlin.math.max | ||
|
|
||
| class Solution { | ||
| fun minimumBoxes(apple: IntArray, capacity: IntArray): Int { | ||
| val count = IntArray(51) | ||
| var appleSum = 0 | ||
| for (j in apple) { | ||
| appleSum += j | ||
| } | ||
| var reqCapacity = 0 | ||
| var max = 0 | ||
| for (j in capacity) { | ||
| count[j]++ | ||
| max = max(max.toDouble(), j.toDouble()).toInt() | ||
| } | ||
| for (i in max downTo 0) { | ||
| if (count[i] >= 1) { | ||
| while (count[i] != 0) { | ||
| appleSum -= i | ||
| reqCapacity++ | ||
| if (appleSum <= 0) { | ||
| return reqCapacity | ||
| } | ||
| count[i]-- | ||
| } | ||
| } | ||
| } | ||
| return reqCapacity | ||
| } | ||
| } |
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,34 @@ | ||
| 3074\. Apple Redistribution into Boxes | ||
|
|
||
| Easy | ||
|
|
||
| You are given an array `apple` of size `n` and an array `capacity` of size `m`. | ||
|
|
||
| There are `n` packs where the <code>i<sup>th</sup></code> pack contains `apple[i]` apples. There are `m` boxes as well, and the <code>i<sup>th</sup></code> box has a capacity of `capacity[i]` apples. | ||
|
|
||
| Return _the **minimum** number of boxes you need to select to redistribute these_ `n` _packs of apples into boxes_. | ||
|
|
||
| **Note** that, apples from the same pack can be distributed into different boxes. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** apple = [1,3,2], capacity = [4,3,1,5,2] | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** We will use boxes with capacities 4 and 5. It is possible to distribute the apples as the total capacity is greater than or equal to the total number of apples. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** apple = [5,5,5], capacity = [2,4,2,7] | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** We will need to use all the boxes. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `1 <= n == apple.length <= 50` | ||
| * `1 <= m == capacity.length <= 50` | ||
| * `1 <= apple[i], capacity[i] <= 50` | ||
| * The input is generated such that it's possible to redistribute packs of apples into boxes. |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
This image is missing a text alternative. This is a problem for people using screen readers.