Top 30 patterns that can be used to solve most of the coding interview questions, with matching leetcode questions
To Write
- ...
- Coding Interview Patterns
- Coding Interview Gym
- iOS Interview Gym
- Behavioural Interview Gym
- System Design Interview Gym
- Object Oriented Design Interview Gym
Detailed explanations with leetcode examples
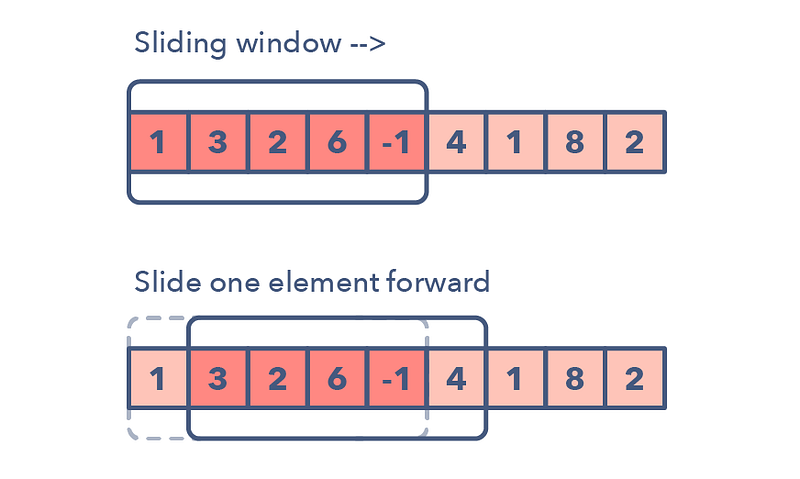
The Sliding Window pattern is used to perform a required operation on a specific window size of a given array or linked list, such as finding the longest subarray containing all 1s. Sliding Windows start from the 1st element and keep shifting right by one element and adjust the length of the window according to the problem that you are solving. In some cases, the window size remains constant and in other cases the sizes grows or shrinks.
📌 Following are some ways you can identify that the given problem might require a sliding window:
- The problem input is a linear data structure such as a linked list, array, or string
- You’re asked to find the longest/shortest substring, subarray, or a desired value
📌 Following are some properties of sliding window:
- Time complexity should not be more than O(N)
- Increasing the "windowEnd" pointer should increase the result/condition, and decreasing "windowStart" pointer should decrease the result/condition.
📌 Common problems you use the sliding window pattern with:
- Maximum sum subarray of size ‘K’ (easy)
- Longest substring with ‘K’ distinct characters (medium)
- String anagrams (hard)
📌 Some important links:
- General summary of what kind of problem can/ cannot solved by Two Pointers
- Why not use Sliding Window algorithm to solve this ?
- How to Solve Sliding Window Problems
- The Sliding Window Algorithm and Similar Techniques
Detailed explanations with leetcode examples
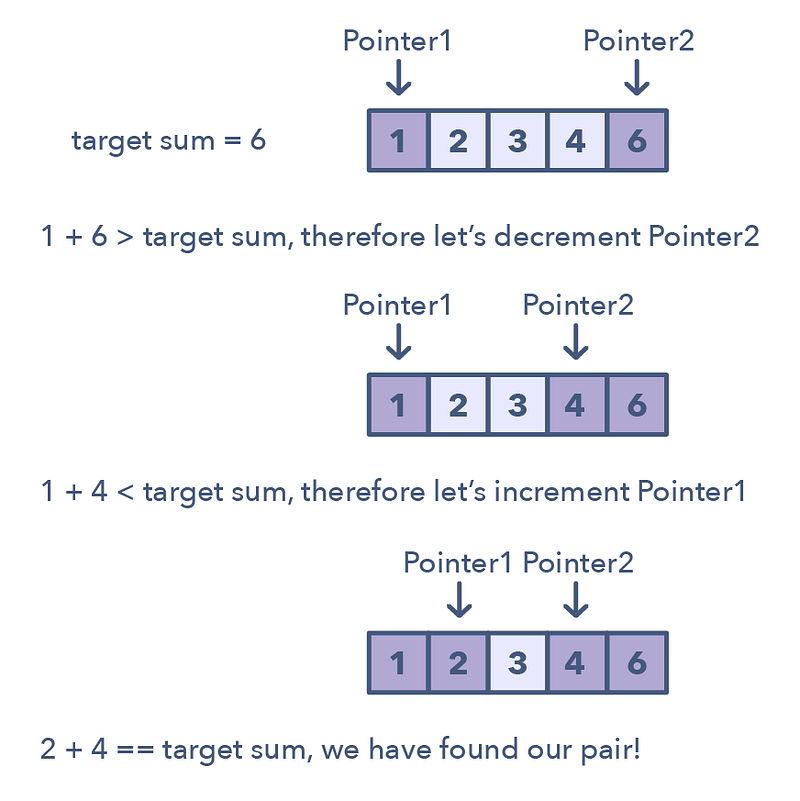
Two Pointers is a pattern where two pointers iterate through the data structure in tandem until one or both of the pointers hit a certain condition. Two Pointers is often useful when searching pairs in a sorted array or linked list; for example, when you have to compare each element of an array to its other elements.
Two pointers are needed because with just pointer, you would have to continually loop back through the array to find the answer. This back and forth with a single iterator is inefficient for time and space complexity — a concept referred to as asymptotic analysis. While the brute force or naive solution with 1 pointer would work, it will produce something along the lines of O(n²). In many cases, two pointers can help you find a solution with better space or runtime complexity.
📌 Ways to identify when to use the Two Pointer method:
- It will feature problems where you deal with sorted arrays (or Linked Lists) and need to find a set of elements that fulfill certain constraints
- The set of elements in the array is a pair, a triplet, or even a subarray
📌 Here are some problems that feature the Two Pointer pattern:
- Squaring a sorted array (easy)
- Triplets that sum to zero (medium)
- Comparing strings that contain backspaces (medium)
📌 Some important links:
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 167. Two Sum II - Input array is sorted | Python | --- | Easy | 📌 Two pointer basics |
| 02 | 1099. Two Sum Less Than K | Python | --- | Easy | 📌 Two pointer basics |
| 03 | 26. Remove Duplicates from Sorted Array | Python | --- | Easy | Two pointer basics |
| 04 | 977. Squares of a Sorted Array | Python | --- | Easy | Two pointer basics |
| 05 | 15. 3Sum | Python | --- | Medium | 📌 Two pointer basics |
| 06 | 16. 3Sum Closest | Python | --- | Medium | 📌 Two pointer basics |
| 07 | 259. 3Sum Smaller | Python | --- | Medium | 📌 Two pointer basics |
| 09 | 713. Subarray Product Less Than K | Python | --- | Medium | Two pointer ad Sliding Window |
| 10 | 75. Sort Colors | Python | Vid 1 | Medium | Two pointer |
| 11 | 18. 4Sum | Python | --- | Medium | Two pointer |
| 12 | 844. Backspace String Compare | Python | --- | Medium | 📌 Two Pointer |
| 13 | 11. Container With Most Water | Python | --- | Medium | Two pointer |
| 14 | 42. Trapping Rain Water | Python | Article 01 | Hard | 📌 Two pointers |
Detailed explanations with leetcode examples
Prefix Sum is a variation of Dynamic Programming. Prefix sum is the cumulative sum of a sequence of numbers a0, a1, ... . It is itself a sequence of numbers b0, b1, ... such that
PreSum0 = a0 PreSum1 = a0 + a1 = PreSum0 + a1 PreSum2 = a0 + a1 + a2 = PreSum1 + a2 . . . . . . . . . PreSumn=PreSumn-1+an
Prefix sum operations can be generalized to any binary operator ⊕. Prefix sum operation takes a sequence of n elements [a0, a1, ..., an] and returns a sequence [a0, (a0 ⊕ a1) , ... , (a0 ⊕ a1 ⊕ a2 ... ⊕ an) ] containing the prefix sums.
For example:
A[] = {1,3,4,5,2,7,8,11} The prefix sums corresponding to A will be PreSum[] = {1,4,8,13,15,22,30,41}
Pseudocode for calculating prefix sums:
A is a sequence containing n elements
PreSum[0]=A[0]
for i=1 to n-1
PreSum[i]=PreSum[i-1]+A[i]Prefix sums can be used to calculate the sum of elements in a given range. If we wish to find out the sum of values between [L..R] we can obtain the sum by subtracting the prefix sum PreSum[R] by PreSum[L-1].
Sum[L..R] = PreSum[R]-PreSum[L-1] { If L!=0 } Sum[L..R] = PreSum[R] { If L=0 }
📌 How do you identify when to use the Prefix Sum pattern?
- You will be asked to find the sum of a range in a array
- If the problem askes to find the contigious sub array of something and the original array isn't sorted and containg negative numbers.
📌 When should I use it over the Two Pointer method mentioned above?
- When the array contains negative numbers.
📌 Problems featuring the PreFix Sum pattern:
- Range Sum Query (Easy)
- Subarray Sum Equals K (medium)
- Number of Submatrices That Sum to Target (hard)
📌 Some important links:
- Prefix Sum
- Why You Must Learn Prefix Sum Algorithm? | Need of prefix-sum Algorithm
- Prefix Sum Algorithm | Prefix Sum Array | Difference Array | Range Sum QueryO(1)
- Algorithms: How Prefix Sums Can Help Improving Operations Over Arrays
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 303. Range Sum Query - Immutable | Python | Vid 1 | Easy | --- |
| 02 | 560. Subarray Sum Equals K | Python | Art 1, Art 2, Art 3, Art 4, Art 5, Art 6 | Medium | Very tricky and persuasive with Sliding Window but it's not. This is a classic running sum problem |
| 03 | 325. Maximum Size Subarray Sum Equals k | Python | Art 1 | Medium | Very tricky and persuasive with Sliding Window but it's not. This is a classic running sum problem |
| 04 | 1074. Number of Submatrices That Sum to Target | Python | Art 1, Art 2, Art 3, Art 4 | Extremely Hard | Very tricky and hard, check again. Also DP |
| 05 | 437. Path Sum III | Python | Educative.io, Art 1, Art 2 | Medium | 📌 A good example of Prefix Sum and DFS. Very Important |
| 06 | 528. Random Pick with Weight | Python | Vid 1, Art 1 | Medium | Very tricky |
| 07 | 363. Max Sum of Rectangle No Larger Than K | Python, Swift | Vid 1, Vid 2, Art 1, Art 2, Art 3 | Hard | DP and BS. Disn't understand S part. TODO: Check again |
| 08 | 862. Shortest Subarray with Sum at Least K | Python, Swift | Art 1, Art 2, Art 3, Art 4 | Hard | Learned Monotonic Queue. Very interesting problem |
Detailed explanations with leetcode examples
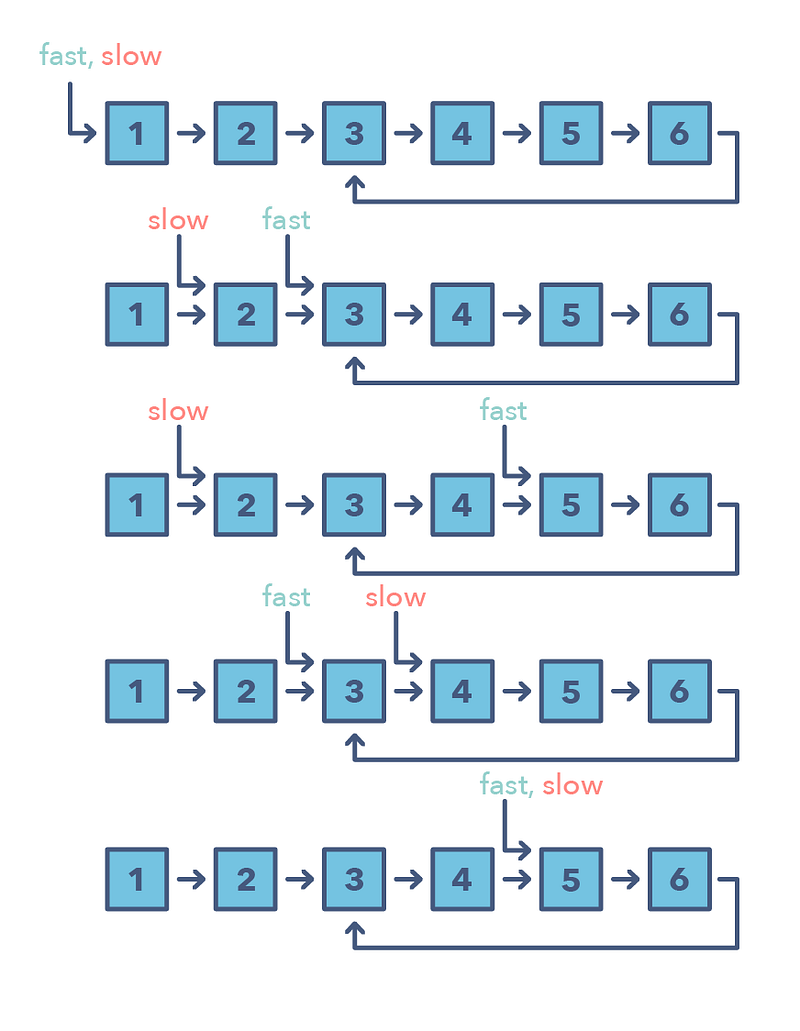
The Fast and Slow pointer approach, also known as the Hare & Tortoise algorithm, is a pointer algorithm that uses two pointers which move through the array (or sequence/linked list) at different speeds. This approach is quite useful when dealing with cyclic linked lists or arrays.
By moving at different speeds (say, in a cyclic linked list), the algorithm proves that the two pointers are bound to meet. The fast pointer should catch the slow pointer once both the pointers are in a cyclic loop.
📌 How do you identify when to use the Fast and Slow pattern?
- The problem will deal with a loop in a linked list or array
- When you need to know the position of a certain element or the overall length of the linked list.
📌 When should I use it over the Two Pointer method mentioned above?
- There are some cases where you shouldn’t use the Two Pointer approach such as in a singly linked list where you can’t move in a backwards direction. An example of when to use the Fast and Slow pattern is when you’re trying to determine if a linked list is a palindrome.
📌 Problems featuring the fast and slow pointers pattern:
- Linked List Cycle (easy)
- Palindrome Linked List (medium)
- Cycle in a Circular Array (hard)
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 141. Linked List Cycle | Python | --- | Easy | Fast pointer Slow pointer |
| 02 | 142. Linked List Cycle II | Python | Art 1, Art 2, AlgoExpert.io | Medium | Fast pointer Slow pointer |
| 03 | 202. Happy Number | Python | Art 1 | Easy | Fast pointer Slow pointer |
| 04 | 876. Middle of the Linked List | Python | --- | Easy | Fast pointer Slow pointer |
| 05 | 234. Palindrome Linked List | Python | --- | Easy | Fast pointer Slow pointer |
| 06 | 143. Reorder List | Python | --- | Medium | Fast pointer Slow pointer |
| 07 | 457. Circular Array Loop | Python | --- | Medium | Fast pointer Slow pointer. Check again |
| 08 | 19. Remove Nth Node From End of List | Python | --- | Medium | Fast pointer Slow pointer |
| 09 | 283. Move Zeroes | Python, Swift | --- | Easy | Not so easy and intuitive. Uses fast and slow pointer |
Detailed explanations with leetcode examples
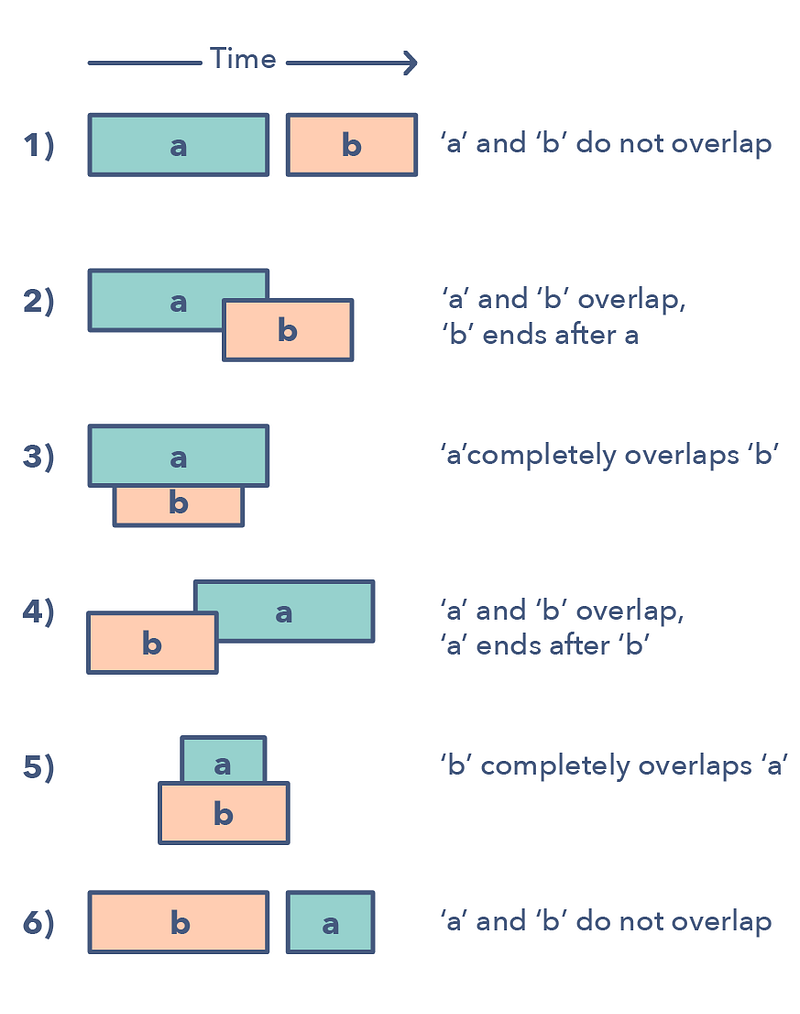
The Merge Intervals pattern is an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, you either need to find overlapping intervals or merge intervals if they overlap. The pattern works like this:
Given two intervals (‘a’ and ‘b’), there will be six different ways the two intervals can relate to each other:
Understanding and recognizing these six cases will help you help you solve a wide range of problems from inserting intervals to optimizing interval merges.
📌 How do you identify when to use the Merge Intervals pattern?
- If you’re asked to produce a list with only mutually exclusive intervals
- If you hear the term “overlapping intervals”.
📌 Merge interval problem patterns:
- Intervals Intersection (medium)
- Maximum CPU Load (hard)
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 56. Merge Intervals | Python | Article | ||
| 02 | 57. Insert Interval | Python | Must | Hard | Greedy and Merge interval |
| 03 | 986. Interval List Intersections | Python | --- | Medium | Greedy and Two Pointer |
| 04 | 252. Meeting Rooms | Python | Official | Easy | Greedy and uses heap |
| 05 | 253. Meeting Rooms II | Python | Official | Medium | Greedy and uses heap |
| 06 | 621. Task Scheduler | Python | Ex 1, Ex 2, Vid 1, Vid 2, Vid 3, Vid 4 | Medium | 📌 Extremely tricky. Classic problem |
| 07 | 435. Non-overlapping Intervals | Python | Vid 1, Art 1 | Medium | Classic problem |
| 08 | 759. Employee Free Time | Python | Educative.io | Hard | Greedy and uses heap. Not done. Check again |
| 09 | 616. Add Bold Tag in String | Python, Swift | --- | Medium | Merge intervals(hidden) |
| 10 | 731. My Calendar II | Python, Swift | Medium | Merge interval |
Detailed explanations with leetcode examples
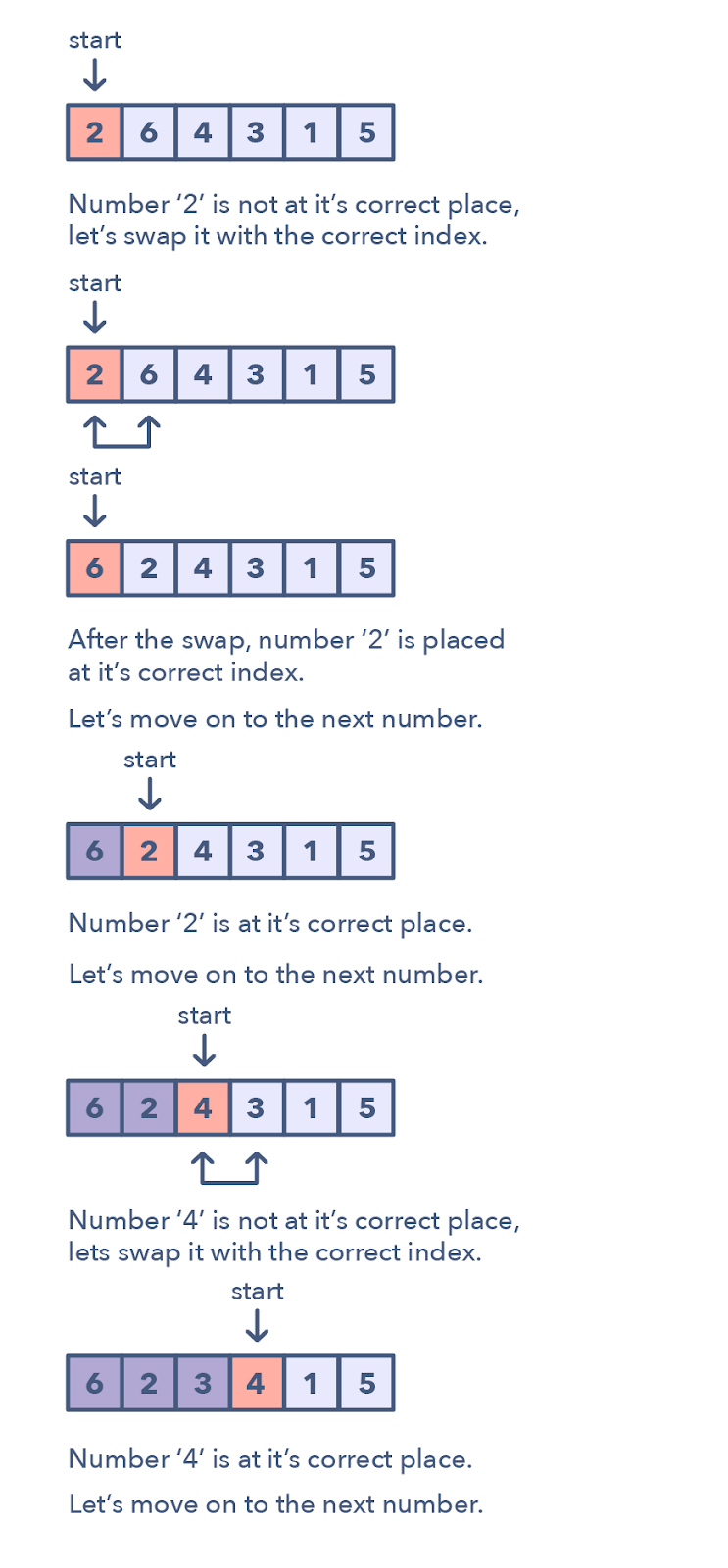
This pattern describes an interesting approach to deal with problems involving arrays containing numbers in a given range. The Cyclic Sort pattern iterates over the array one number at a time, and if the current number you are iterating is not at the correct index, you swap it with the number at its correct index. You could try placing the number in its correct index, but this will produce a complexity of O(n^2) which is not optimal, hence the Cyclic Sort pattern.
📌 How do I identify this pattern?
- They will be problems involving a sorted array with numbers in a given range
- If the problem asks you to find the missing/duplicate/smallest number in an sorted/rotated array
- There will be a certain relation between the array indexxes and it's actual associated values
📌 Problems featuring cyclic sort pattern:
- Find the Missing Number (easy)
- Find the Smallest Missing Positive Number (medium)
📌 Some important links:
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 268. Missing Number | Python | Official | Easy | 📌 Also check Bit manipulation where I learned few very important binary logic properties |
| 02 | 448. Find All Numbers Disappeared in an Array | Python | --- | Easy | Cyclic Sort |
| 03 | 287. Find the Duplicate Number | Python | --- | Medium | Cyclic Sort. TODO: Check all other approaches |
| 04 | 442. Find All Duplicates in an Array | Python | --- | Medium | Cyclic Sort TODO: Check all other approaches |
| 05 | 41. First Missing Positive | Python | --- | Hard | Cyclic Sort, Very important |
Detailed explanations with leetcode examples
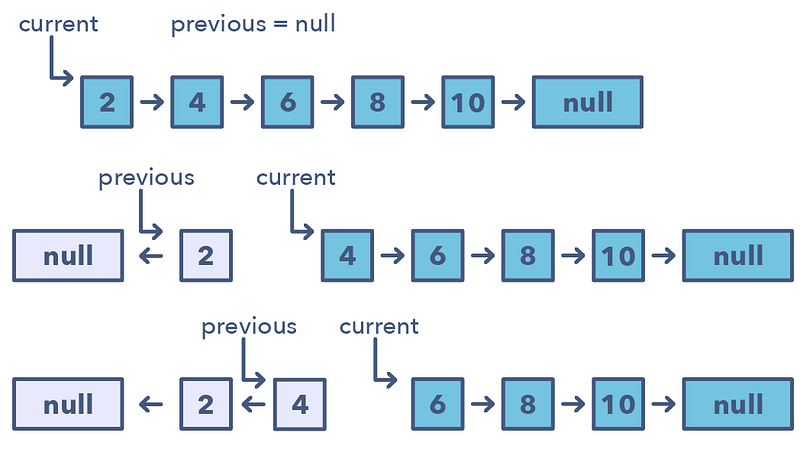
In a lot of problems, you may be asked to reverse the links between a set of nodes of a linked list. Often, the constraint is that you need to do this in-place, i.e., using the existing node objects and without using extra memory. This is where the above mentioned pattern is useful.
This pattern reverses one node at a time starting with one variable (current) pointing to the head of the linked list, and one variable (previous) will point to the previous node that you have processed. In a lock-step manner, you will reverse the current node by pointing it to the previous before moving on to the next node. Also, you will update the variable “previous” to always point to the previous node that you have processed.
📌 How do I identify when to use this pattern:
- If you’re asked to reverse a linked list without using extra memory
📌 Problems featuring in-place reversal of linked list pattern:
- Reverse a Sub-list (medium)
- Reverse every K-element Sub-list (medium)
Detailed explanations with leetcode examples
This pattern is based on the Breadth First Search (BFS) technique to traverse a tree and uses a queue to keep track of all the nodes of a level before jumping onto the next level. Any problem involving the traversal of a tree in a level-by-level order can be efficiently solved using this approach.
The Tree BFS pattern works by pushing the root node to the queue and then continually iterating until the queue is empty. For each iteration, we remove the node at the head of the queue and “visit” that node. After removing each node from the queue, we also insert all of its children into the queue.
📌 How to identify the Tree BFS pattern:
- If you’re asked to traverse a tree in a level-by-level fashion (or level order traversal)
📌 Problems featuring Tree BFS pattern:
- Binary Tree Level Order Traversal (easy)
- Zigzag Traversal (medium)
Detailed explanations with leetcode examples
Tree DFS is based on the Depth First Search (DFS) technique to traverse a tree.
You can use recursion (or a stack for the iterative approach) to keep track of all the previous (parent) nodes while traversing.
The Tree DFS pattern works by starting at the root of the tree, if the node is not a leaf you need to do three things:
Decide whether to process the current node now (pre-order), or between processing two children (in-order) or after processing both children (post-order). Make two recursive calls for both the children of the current node to process them.
📌 How to identify the Tree DFS pattern:
- If you’re asked to traverse a tree with in-order, preorder, or postorder DFS
- If the problem requires searching for something where the node is closer to a leaf
📌 Problems featuring Tree DFS pattern:
- Sum of Path Numbers (medium)
- All Paths for a Sum (medium)
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 112. Path Sum | Python | Art 1 | Easy | --- |
| 02 | 113. Path Sum II | Python | Art 1, Art 2 | Medium | --- |
| 03 | 437. Path Sum III | Python | Educative.io, Art 1, Art 2 | Medium | 📌 A good example of Prefix Sum and DFS. Very Important |
| 04 | 543. Diameter of Binary Tree | Python | Educative.io, Art 1 | Medium | 📌 Important |
| 05 | 124. Binary Tree Maximum Path Sum | Python | Art 1, Art 2, Vid 1, AlgoExpert | Very Hard | Very important and tricky |
Detailed explanations with leetcode examples
In many problems, we are given a set of elements such that we can divide them into two parts. To solve the problem, we are interested in knowing the smallest element in one part and the biggest element in the other part. This pattern is an efficient approach to solve such problems.
This pattern uses two heaps; A Min Heap to find the smallest element and a Max Heap to find the biggest element. The pattern works by storing the first half of numbers in a Max Heap, this is because you want to find the largest number in the first half. You then store the second half of numbers in a Min Heap, as you want to find the smallest number in the second half. At any time, the median of the current list of numbers can be calculated from the top element of the two heaps.
📌 Ways to identify the Two Heaps pattern:
- Useful in situations like Priority Queue, Scheduling
- If the problem states that you need to find the smallest/largest/median elements of a set
- Sometimes, useful in problems featuring a binary tree data structure
📌 Problems featuring
- Find the Median of a Number Stream (medium)
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 295. Find Median from Data Stream | Python | algoexpert.io, educative.io, codinginterviewclass.com, Official, FollowUp 1 | Hard | 📌 Very Tricky and important. TODO: Check again |
| 02 | 480. Sliding Window Median | Python | educative.io, Vid 1 | Hard | 📌 Sliding window with 2 heap. very important |
| 03 | 4. Median of Two Sorted Arrays | Python | Article 01, Art 2 Video 1 | Hard | 📌 Classic problem |
Detailed explanations with leetcode examples
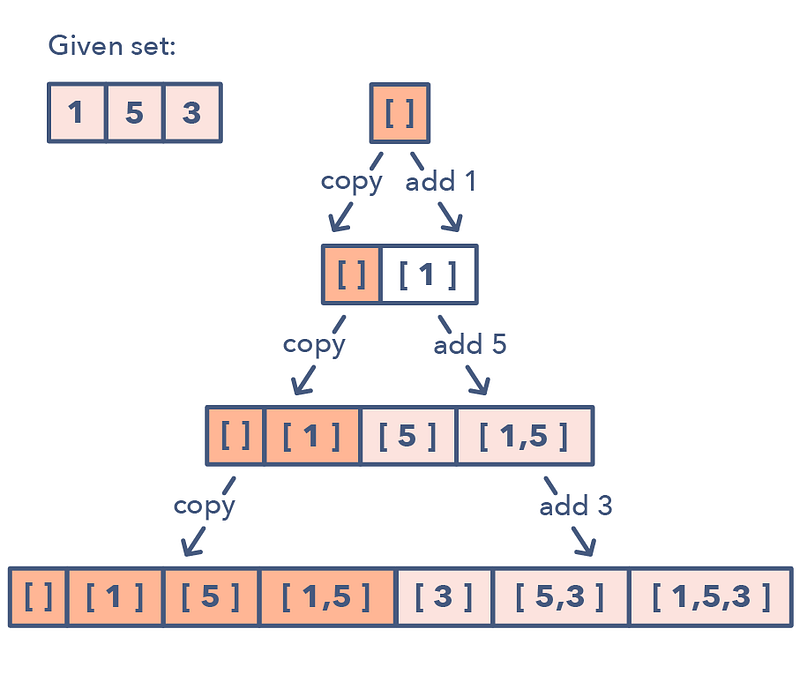
A huge number of coding interview problems involve dealing with Permutations and Combinations of a given set of elements. The pattern Subsets describes an efficient Breadth First Search (BFS) approach to handle all these problems.
📌 The pattern looks like this:
Given a set of [1, 5, 3]
- Start with an empty set: [[]]
- Add the first number (1) to all the existing subsets to create new subsets: [[], [1]];
- Add the second number (5) to all the existing subsets: [[], [1], [5], [1,5]];
- Add the third number (3) to all the existing subsets: [[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3]].
- Here is a visual representation of the Subsets pattern:
📌 How to identify the Subsets pattern:
- Problems where you need to find the combinations or permutations of a given set
📌 Problems featuring Subsets pattern:
- Subsets With Duplicates (easy)
- String Permutations by changing case (medium)
Detailed explanations with leetcode examples
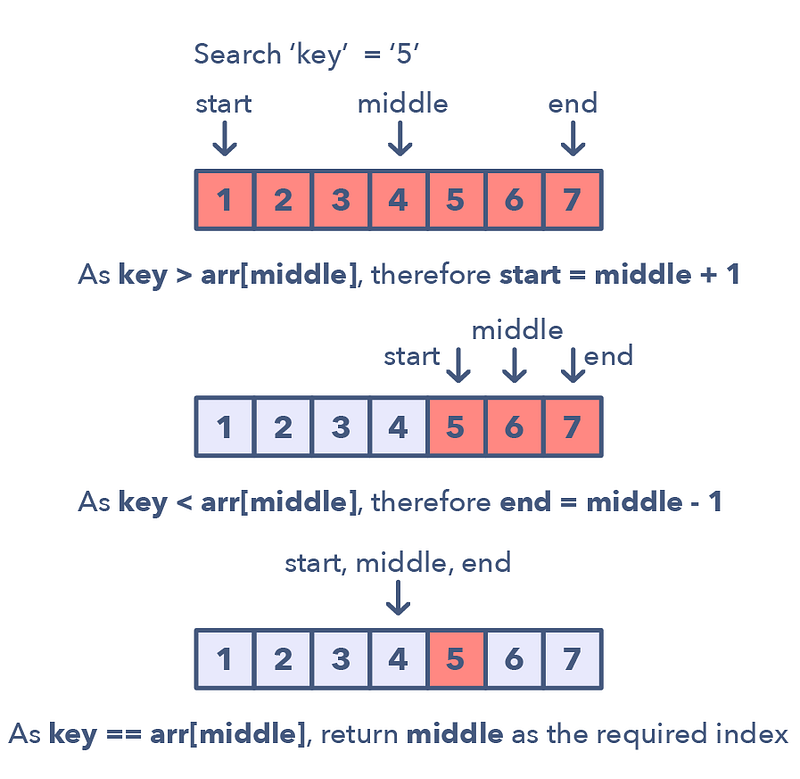
Whenever you are given a sorted array, or matrix, and are asked to find a certain element, the best algorithm you can use is the Binary Search. This pattern describes an efficient way to handle all problems involving Binary Search.
📌 The patterns looks like this for an ascending order set:
- First, find the middle of start and end. An easy way to find the middle would be: middle = (start + end) / 2. But this has a good chance of producing an integer overflow so it’s recommended that you represent the middle as: middle = start + (end — start) / 2
- If the key is equal to the number at index middle then return middle
- If ‘key’ isn’t equal to the index middle:
- Check if key < arr[middle]. If it is reduce your search to end = middle — 1
- Check if key > arr[middle]. If it is reduce your search to start = middle + 1
Here is a visual representation of the Modified Binary Search pattern:
📌 Problems featuring the Modified Binary Search pattern:
- Order-agnostic Binary Search (easy)
- Search in a Sorted Infinite Array (medium)
Detailed explanations with leetcode examples
XOR is a logical bitwise operator that returns 0 (false) if both bits are the same and returns 1 (true) otherwise. In other words, it only returns 1 if exactly one bit is set to 1 out of the two bits in comparison.
| A | B | A xor B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
It is surprising to know the approaches that the XOR operator enables us to solve certain problems.
📌 Please check thefollowing and go through to understand this patter a it more details.
- XOR - The magical bitwise operator
- Bit Manipulation - youtube
- Your guide to Bit Manipulation
- Python Bitwise Operators
- Binary Arithmetic
- 1’s and 2’s complement of a Binary Number
- A summary: how to use bit manipulation to solve problems easily and efficiently - leetcode
- What is Bit Masking?
- Understanding Bit masks
- Bitmasks: A very esoteric (and impractical) way of managing booleans
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 268. Missing Number | Python | Educative.io, Official | Easy | 📌 Learned few very important binary logic properties. Also check cyclic sort technique |
| 02 | 136. Single Number | Python | Educative.io | Easy | 📌 The key here is to practice bit operation, i ignore any other attempts |
| 03 | 137. Single Number II | Python | 1, 2, 3, Check discussion | Medium | ⭐ 😭 Didn't understand, check again |
| 04 | 260. Single Number III | Python | Educative.io | Medium | ⭐ 😭 Check again, very important |
| 05 | 476. Number Complement | Python | Educative.io | Easy | ⭐ Check again |
| 06 | 832. Flipping an Image | Python | Educative.io | Easy | ⭐ Check again |
Detailed explanations with leetcode examples
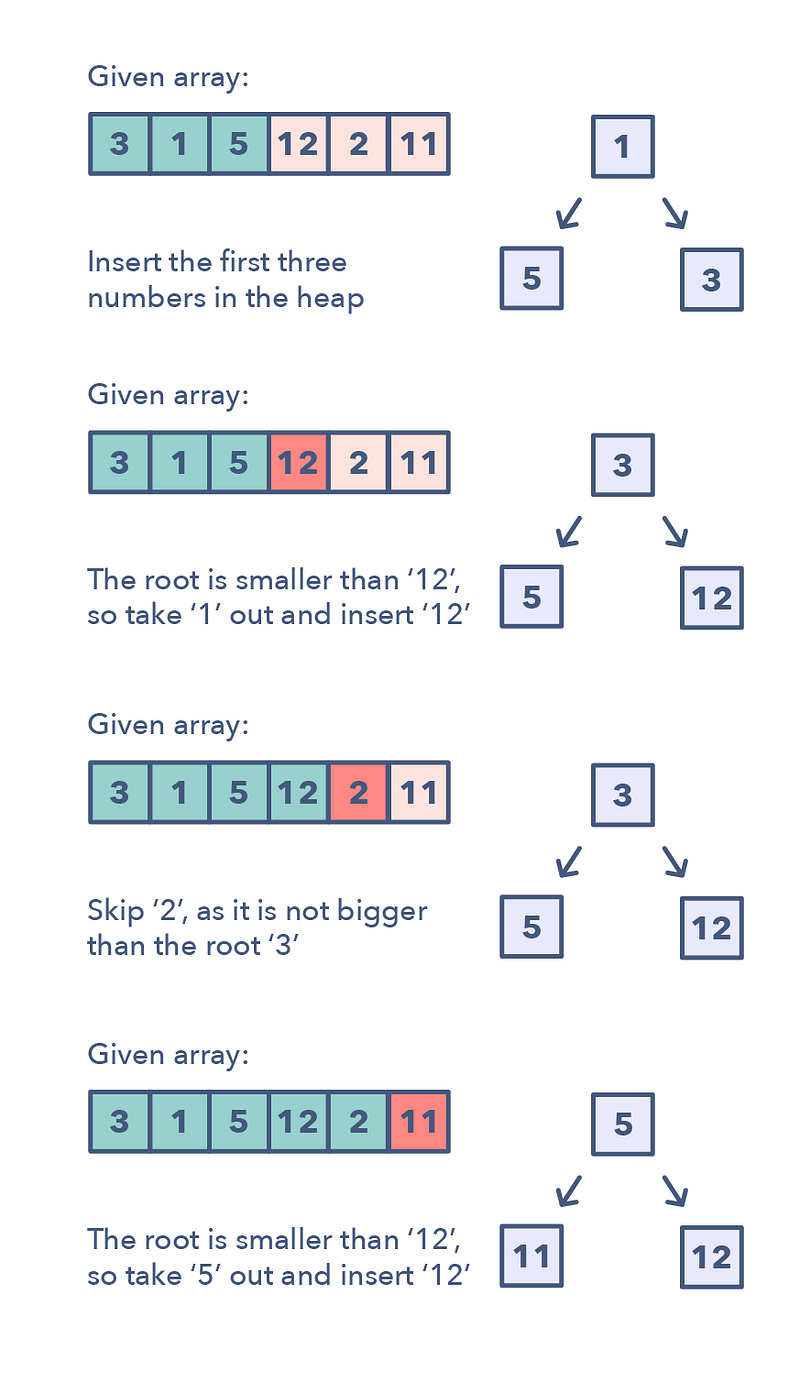
Any problem that asks us to find the top/smallest/frequent ‘K’ elements among a given set falls under this pattern.
The best data structure to keep track of ‘K’ elements is Heap. This pattern will make use of the Heap to solve multiple problems dealing with ‘K’ elements at a time from a set of given elements.
📌 The pattern looks like this:
- Insert ‘K’ elements into the min-heap or max-heap based on the problem.
- Iterate through the remaining numbers and if you find one that is larger than what you have in the heap, then remove that number and insert the larger one.
There is no need for a sorting algorithm because the heap will keep track of the elements for you.
📌 How to identify the Top ‘K’ Elements pattern:
- If you’re asked to find the top/smallest/frequent ‘K’ elements of a given set
- If you’re asked to sort an array to find an exact element
📌 Problems featuring Top ‘K’ Elements pattern:
- Top ‘K’ Numbers (easy)
- Top ‘K’ Frequent Numbers (medium)
Detailed explanations with leetcode examples
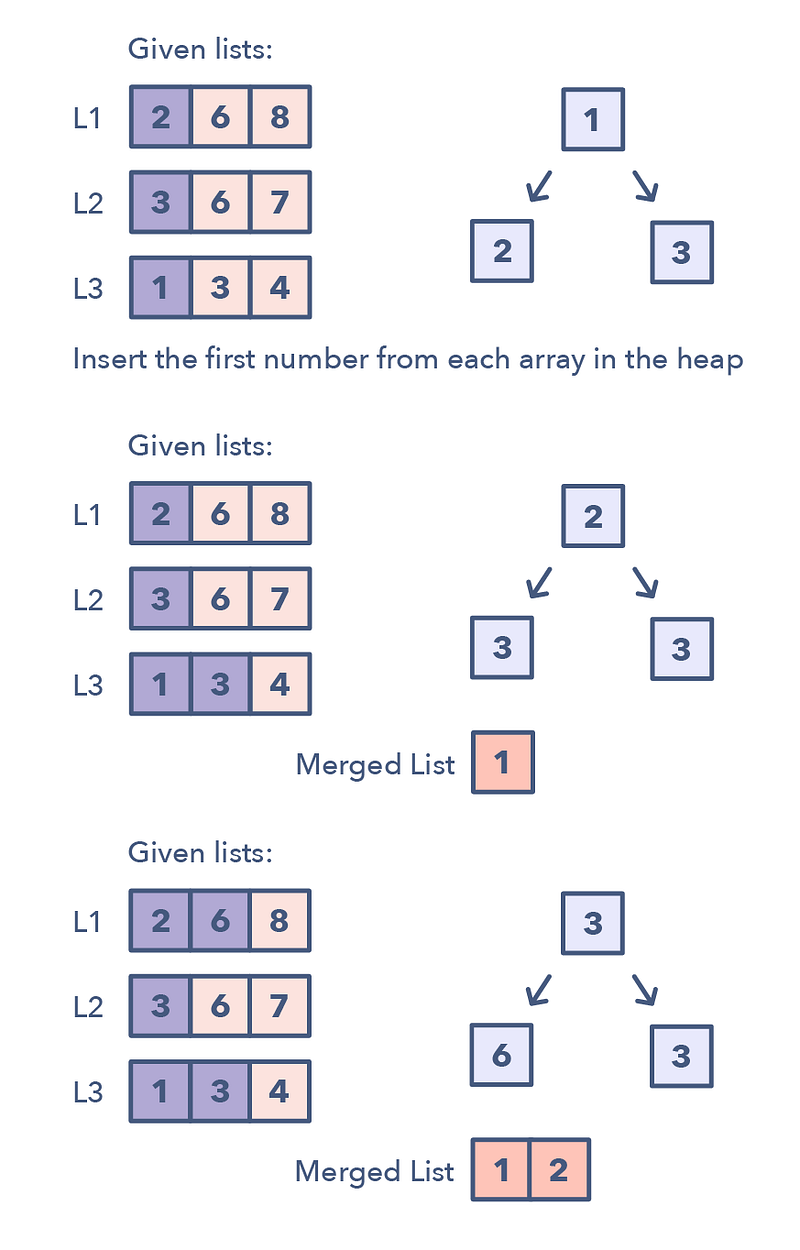
K-way Merge helps you solve problems that involve a set of sorted arrays.
Whenever we are given ‘K’ sorted arrays, we can use a Heap to efficiently perform a sorted traversal of all the elements of all arrays. We can push the smallest (first) element of each sorted array in a Min Heap to get the overall minimum. While inserting elements to the Min Heap we keep track of which array the element came from. We can, then, remove the top element from the heap to get the smallest element and push the next element from the same array, to which this smallest element belonged, to the heap. We can repeat this process to make a sorted traversal of all elements.
📌 The pattern looks like this:
- Insert the first element of each array in a Min Heap.
- After this, take out the smallest (top) element from the heap and add it to the merged list.
- After removing the smallest element from the heap, insert the next element of the same list into the heap.
- Repeat steps 2 and 3 to populate the merged list in sorted order.
📌 How to identify the K-way Merge pattern:
- The problem will feature sorted arrays, lists, or a matrix
- If the problem asks you to merge sorted lists, find the smallest element in a sorted list.
📌 Problems featuring the K-way Merge pattern:
- Merge K Sorted Lists (medium)
- K Pairs with Largest Sums (Hard)
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 23. Merge k Sorted Lists | Python | educative.io, Art 1 | Hard | Very important. TODO: Check heap approach |
| 02 | 378. Kth Smallest Element in a Sorted Matrix | Python | educative.io | Hard | 📌 TODO: Check again the Binary Search approach. Very important |
| 03 | 632. Smallest Range Covering Elements from K Lists | Python | educative.io | Hard | 📌 TODO: Check again. Very important |
| 04 | 373. Find K Pairs with Smallest Sums | Python | educative.io | Hard | 📌 TODO: Check again. |
Detailed explanations with leetcode examples
Topological Sort is used to find a linear ordering of elements that have dependencies on each other. For example, if event ‘B’ is dependent on event ‘A’, ‘A’ comes before ‘B’ in topological ordering.
This pattern defines an easy way to understand the technique for performing topological sorting of a set of elements.
📌 The pattern works like this:
- Initialization
- a) Store the graph in adjacency lists by using a HashMap
- b) To find all sources, use a HashMap to keep the count of in-degrees
- Build the graph and find in-degrees of all vertices
- a) Build the graph from the input and populate the in-degrees HashMap.
- Find all sources
- a) All vertices with ‘0’ in-degrees will be sources and are stored in a Queue.
- Sort
-
a) For each source, do the following things:
-
- Add it to the sorted list. - 2) Get all of its children from the graph. - 3) Decrement the in-degree of each child by 1.
-
- If a child’s in-degree becomes ‘0’, add it to the sources Queue.
-
-
b) Repeat (a), until the source Queue is empty.
-
📌 How to identify the Topological Sort pattern:
- The problem will deal with graphs that have no directed cycles
- If you’re asked to update all objects in a sorted order
- If you have a class of objects that follow a particular order
📌 Problems featuring the Topological Sort pattern:
- Task scheduling (medium)
- Minimum height of a tree (hard)
📌 Some importanr referrences and further study materials
- Topological Sort Algorithm | Graph Theory | Youtube
- Topological Sorting | GeeksforGeeks | Youtube
- Topological Sort Graph Algorithm | Youtube
- Codinginterviewclass.com
- Algoexpert.io
- Educative.io
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 207. Course Schedule | Python | educative.io | Medium | 📌 Very Important. Check again. BFS, Topological Sort |
| 02 | 210. Course Schedule II | Python | educative.io | Medium | 📌 Very Important. Check again. BFS, Topological Sort |
| 03 | 269. Alien Dictionary | Python | educative.io, Vid 1, Vid 2, Vid 3 | Hard | 📌 Very Important. Check again. BFS, Topological Sort |
| 04 | 444. Sequence Reconstruction | Python | educative.io | Medium/Hard | 📌 Check again. BFS, Topological Sort |
| 05 | 310. Minimum Height Trees | Python | educative.io | Hard | 📌 TODO: Check again, very hard, didn't get the intuition. BFS, Topological Sort |
| 06 | 329. Longest Increasing Path in a Matrix | Python | Official, Art 1, Art 2 | Hard | ** 📌 TODO: Not Done, very hard and important. DP, Topological Sort ** |
| 07 | 1203. Sort Items by Groups Respecting Dependencies | Python | Hard | 📌 TODO: Not Done, very hard, didn't get the intuition. BFS, Topological Sort | |
| 08 | 1136. Parallel Courses | Python, Swift | --- | Hard | 📌 Topological sort. |
Detailed explanations with leetcode examples
📌 What is Union Find(Disjoint-set) data structure?
- Represents a mathematics concept Set.
- A disjoint-set data structure, also called a union–find data structure or merge–find set.
- A disjoint-set data structure that keeps track of a set of elements partitioned into a number of disjoint or non-overlapping subsets.
- It provides near-constant-time operations to add new sets, to merge existing sets, and to determine whether elements are in the same set.
- Plays a key role in Kruskal’s algorithm for finding the minimum spanning tree of a graph.
- This can also be used to detect cycle in the graph.
📌 How Disjoint Set is constructed:
- A disjoint-set forest consists of a number of elements each of which stores an id, a parent pointer
- The parent pointers of elements are arranged to form one or more trees, each representing a set.
- If an element’s parent pointer points to no other element, then the element is the root of a tree and is the representative member of its set.
- A set may consist of only a single element. However, if the element has a parent, the element is part of whatever set is identified by following the chain of parents upwards until a representative element (one without a parent) is reached at the root of the tree.
📌 Disjoint Set Operations:
-
MakeSet(X): This operation makes a new set by creating a new element with a parent pointer to itself. The parent pointer to itself indicates that the element is the representative member of its own set. The MakeSet operation has O(1) time complexity.
-
Find(X): follows the chain of parent pointers from x upwards through the tree until an element is reached whose parent is itself. This element is the root of the tree and is the representative member of the set to which x belongs, and may be x itself.
-
Union(x,y): Uses Find to determine the roots of the trees x and y belong to. If the roots are distinct, the trees are combined by attaching the root of one to the root of the other. If this is done naively, such as by always making x a child of y, the height of the trees can grow as O(n).
📌 Some important referrences and further study materials
- Union Find [Disjoint Set] Playlist
- Disjoint Sets Data Structure - Weighted Union and Collapsing Find
- Disjoint Sets Data Structure - Topcoder
- Disjoint Sets using union by rank and path compression Graph Algorithm
- Disjoint Set Data Structure – Union Find Algorithm
- Disjoint Set | Union-Find Algorithm – Union by rank and path compression
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 200. Number of Islands | Python | Algoexpert.io - DFS, Union Find | Medium | DFS + DFS, Union Find |
| 02 | 305. Number of Islands II | Python | Union Find, Art 0, Art 1, Art 2, Art 3, Art 4, Art 5 | Hard | Union Find |
| 03 | 947. Most Stones Removed with Same Row or Column | Python, Swift | Vid 1, Art 1, Vid 2, Art 2, Art 3 | Medium | 📌 DFS and Union FInd |
| # | Solve at least 10 more problems form this list using Uion Find | --- | --- | --- | --- |
Detailed explanations with leetcode examples
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 332. Reconstruct Itinerary | Python | Vid 1, Vid 2, Art 1, Art 2, Art 3, Art 4 | Medium | Important, Learned new things. Directed Graph. Eulerian path and top Sort |
| 02 | 743. Network Delay Time | Python | Official, Dijkstra 1, Dijkstra 2, Vid 1, Art 1, Art 2, Art 3, Art 4 | Medium | TODO: Check again. Very Important. Learned (Dijkstra, Bellman, Floyed). Check references section |
| 03 | 1168. Optimize Water Distribution in a Village | Python | Art 1, Art 2, Art 3, Art 4 | Hard | TODO: Check AGain. Prim's and Kruskal's algorithm. Important. |
| 04 | 1066. Campus Bikes II | Python | Vid 1, Art 1 | Medium | 📌 TODO: CHECK Dijkstra approach again. Backtracking solution is getting TLE. Solve it and implement it with DP also. Very important |
| 05 | 1192. Critical Connections in a Network | Python, Swift | Art 1, Art 2, Art 3, Art 4, Vid 1, Vid 2, Vid 3 | Hard | 📌 Important, Learned new things.Tarjans SCCs algorithm. Check again |
Detailed explanations with leetcode examples
Given the weights and profits of N items, we are asked to put these items in a knapsack which has a capacity C. The goal is to get the maximum profit from the items in the knapsack. Each item can only be selected once, as we don’t have multiple quantities of any item.
Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:
Items: { Apple, Orange, Banana, Melon }
Weights: { 2, 3, 1, 4 }
Profits: { 4, 5, 3, 7 }
Knapsack capacity: 5Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5:
Apple + Orange (total weight 5) => 9 profit
Apple + Banana (total weight 3) => 7 profit
Orange + Banana (total weight 4) => 8 profit
Banana + Melon (total weight 5) => 10 profitThis shows that Banana + Melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.
Given two integer arrays to represent weights and profits of N items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number C. Each item can only be selected once, which means either we put an item in the knapsack or we skip it.
📌 Some very importanr referrences and further study materials
- Knapsack Problem - Greedy Method | Youtube
- Knapsack - Two Methods - Dynamic Programming | Youtube
- Knapsack Problem (Program) - Dynamic Programming | Youtube
- The 0/1 Knapsack Problem | Codinginterviewclass.com
- The 0/1 Knapsack Problem (Demystifying Dynamic Programming) | Youtube
- Educative.io
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 416. Partition Equal Subset Sum | Python | educative.io, Art 1, Vid 1, Vid 2, Vid 3, Vid 4 | Medium | 0/1 Knapsack, Very important |
| 02 | 494. Target Sum | Python | educative.io, MUST MUST READ | Medium | 0/1 Knapsack, Very important. TODO: Not DOne. Check again |
Detailed explanations with leetcode examples
Given the weights and profits of N items, we are asked to put these items in a knapsack which has a capacity C. The goal is to get the maximum profit from the items in the knapsack. The only difference between the 0/1 Knapsack problem and this problem is that we are allowed to use an unlimited quantity of an item.
Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:
Items: { Apple, Orange, Melon }
Weights: { 1, 2, 3 }
Profits: { 15, 20, 50 }
Knapsack capacity: 5Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5.
5 Apples (total weight 5) => 75 profit
1 Apple + 2 Oranges (total weight 5) => 55 profit
2 Apples + 1 Melon (total weight 5) => 80 profit
1 Orange + 1 Melon (total weight 5) => 70 profitThis shows that 2 apples + 1 melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.
Given two integer arrays to represent weights and profits of N items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number C. We can assume an infinite supply of item quantities; therefore, each item can be selected multiple times.
📌 Some very importanr referrences and further study materials
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 518. Coin Change 2 | Python | educative.io, Vid 1, codinginterviewclass.com, Algoexpert.io | Medium | Unbounded Knapsack |
| 02 | 322. Coin Change | Python | educative.io, Vid 1, Algoexpert.io | Medium | Unbounded Knapsack |
| 03 | 343. Integer Break | Python | Art 1, Art 2 | Medium | Unbounded Knapsack. TODO: Not Done. Check again |
Detailed explanations with leetcode examples
Write a function to calculate the nth Fibonacci number.
Fibonacci numbers are a series of numbers in which each number is the sum of the two preceding numbers. First few Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, …
Mathematically we can define the Fibonacci numbers as:
Fib(n) = Fib(n-1) + Fib(n-2), for n > 1
Given that: Fib(0) = 0, and Fib(1) = 1The time complexity of the above algorithm is exponential O(2^n) as we are making two recursive calls in the same function. The space complexity is O(n) which is used to store the recursion stack.
Let’s visually draw the recursion for CalculateFibonacci(4) to see the overlapping subproblems:
We can clearly see the overlapping subproblem pattern:
fib(2) has been called twice and fib(1) has been called thrice. We can optimize this using memoization to store the results for subproblems.
📌 Some very importanr referrences and further study materials
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 70. Climbing Stairs | Python | educative.io | Easy | Fibonacci sequence pattern |
| 02 | 55. Jump Game | Python | Official , Art 1 | Medium | 📌 Must Check. Learned a lot |
| 03 | 45. Jump Game II | Python | educative.io, Vid 1, Vid 2, Vid 3, Art 1 | Hard | 📌 |
| 04 | 198. House Robber | Python | Must, educative.io | Easy | A Gold Mine |
| 05 | 213. House Robber II | Python | Art 1, Art 2 | Medium | --- |
| 06 | 337. House Robber III | Python | Art 1 | Medium | Another gold mine, hidden greedy and DFS |
| 07 | 279. Perfect Squares | Python | Must, Vid 1, Vis 2 | Medium | TODO: Check again. Very Important. Very analytical and tricky to come up with |
Detailed explanations with leetcode examples
There are some problems that deals with Longest/Minimum Common/Increasing/Bitonic/Repeating/Alterating Subsequence/Substring on Palindrome which are generally solved using DP.
General problem statement for this pattern can vary but most of the time you are given one string where length of that string is not big
Given one strings s1, return some result.
Most of the problems on this pattern requires a solution that can be accepted in O(n^2) complexity.
for (int l = 1; l < n; ++l) {
for (int i = 0; i < n-l; ++i) {
int j = i + l;
if (s[i] == s[j]) {
dp[i][j] = /*code*/;
} else {
dp[i][j] = /*code*/;
}
}
}| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 516. Longest Palindromic Subsequence | Python | educative.io, Vid 1, Vid 2 | Medium | --- |
| 02 | 5. Longest Palindromic Substring | Python | educative.io, algoexpert.io, Vid 1 | Medium | 📌 Classic DP |
| 03 | 647. Palindromic Substrings | Python | educative.io | Medium | --- |
| 04 | 680. Valid Palindrome II | Python | educative.io, Art 1, Art 2 | Medium | --- |
| 05 | 1312. Minimum Insertion Steps to Make a String Palindrome | Python | educative.io | Hard | --- |
| 06 | 132. Palindrome Partitioning II | Python | educative.io, algoexpert.io, Vid 1, Vid 2 | Hard | TODO: Check again. Very difficult and important |
Detailed explanations with leetcode examples
There are some problems that deals with Longest/Minimum Common/Increasing/Bitonic/Repeating/Alterating Subsequence/Substring which are generally solved using DP.
General problem statement for this pattern can vary but most of the time you are given two strings where lengths of those strings are not big
Given two strings s1 and s2, return some result.
Most of the problems on this pattern requires a solution that can be accepted in O(n^2) complexity.
// i - indexing string s1
// j - indexing string s2
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (s1[i-1] == s2[j-1]) {
dp[i][j] = /*code*/;
} else {
dp[i][j] = /*code*/;
}
}
}Detailed explanations with leetcode examples
Given a target find minimum (maximum) cost / path / sum to reach the target.
Choose minimum (maximum) path among all possible paths before the current state, then add value for the current state.
routes[i] = min(routes[i-1], routes[i-2], ... , routes[i-k]) + cost[i]
Generate optimal solutions for all values in the target and return the value for the target.
for (int i = 1; i <= target; ++i) {
for (int j = 0; j < ways.size(); ++j) {
if (ways[j] <= i) {
dp[i] = min(dp[i], dp[i - ways[j]]) + cost / path / sum;
}
}
}
return dp[target]| # | Title | Solution | Tutorial | Level | Remarks |
|---|
Detailed explanations with leetcode examples
Given a target find a number of distinct ways to reach the target.
Sum all possible ways to reach the current state.
routes[i] = routes[i-1] + routes[i-2], ... , + routes[i-k]
Generate sum for all values in the target and return the value for the target.
for (int i = 1; i <= target; ++i) {
for (int j = 0; j < ways.size(); ++j) {
if (ways[j] <= i) {
dp[i] += dp[i - ways[j]];
}
}
}
return dp[target]- Some questions point out the number of repetitions, in that case, add one more loop to simulate every repetition.
| # | Title | Solution | Tutorial | Level | Remarks |
|---|
Detailed explanations with leetcode examples
Given a set of numbers find an optimal solution for a problem considering the current number and the best you can get from the left and right sides.
Find all optimal solutions for every interval and return the best possible answer.
// from i to j
dp[i][j] = dp[i][k] + result[k] + dp[k+1][j]Get the best from the left and right sides and add a solution for the current position.
for(int l = 1; l<n; l++) {
for(int i = 0; i<n-l; i++) {
int j = i+l;
for(int k = i; k<j; k++) {
dp[i][j] = max(dp[i][j], dp[i][k] + result[k] + dp[k+1][j]);
}
}
}
return dp[0][n-1]- Some questions point out the number of repetitions, in that case, add one more loop to simulate every repetition.
| # | Title | Solution | Tutorial | Level | Remarks |
|---|
Detailed explanations with leetcode examples
The general problem statement for this pattern is forgiven situation decide whether to use or not to use the current state. So, the problem requires you to make a decision at a current state.
Given a set of values find an answer with an option to choose or ignore the current value.
If you decide to choose the current value use the previous result where the value was ignored; vice-versa, if you decide to ignore the current value use previous result where value was used.
// i - indexing a set of values
// j - options to ignore j values
for (int i = 1; i < n; ++i) {
for (int j = 1; j <= k; ++j) {
dp[i][j] = max({dp[i][j], dp[i-1][j] + arr[i], dp[i-1][j-1]});
dp[i][j-1] = max({dp[i][j-1], dp[i-1][j-1] + arr[i], arr[i]});
}
}for (int i = 1; i < n; ++i) {
dp[i][1] = max(dp[i-1][0] + nums[i], dp[i-1][1]);
dp[i][0] = dp[i-1][1];
}| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 121. Best Time to Buy and Sell Stock | Python | Vid 1 | Easy | Fundamental |
| 02 | 122. Best Time to Buy and Sell Stock II | Python | Video 01 | Easy | More like Greedy |
| 03 | 123. Best Time to Buy and Sell Stock III | Python | Vid 1, Vid 2 | Hard | Fundamental |
| 04 | 188. Best Time to Buy and Sell Stock IV | Python | Vid 1, Vid 2 | Hard | Getting "Memory Limit Exceeded" |
| 05 | 309. Best Time to Buy and Sell Stock with Cooldown | Python | Must, Art0, Art1, Must 2 , Art 2, Art 3 | Medium | Very tricky, must check again. Couldn't solve |
| 06 | 714. Best Time to Buy and Sell Stock with Transaction Fee | Python | Must Read , Art 2 | Medium | More like Greedy, but DP |
| 07 | 198. House Robber | Python | Must, educative.io | Easy | A Gold Mine |
| 08 | 213. House Robber II | Python | Art 1, Art 2 | Medium | --- |
| 09 | 337. House Robber III | Python | Art 1 | Medium | Another gold mine, hidden greedy and DFS |
Detailed explanations with leetcode examples
Given ssome kinds of nested list of of some kinds of data, implement an iterator to iterate through the give data.
An iterator shouldn't copy and modify the entire data but just iterate over the original data structure. And shuld return the data on the fly. Also there should't be any internal dependency among the methods of iterator.
- Some questions point out the number of repetitions, in that case, add one more loop to simulate every repetition.
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 284. Peeking Iterator | Python, Swift | Art 1 | Medium | MUST read |
| 02 | 341. Flatten Nested List Iterator | Python, Swift | Vid 1, Art 1, Art 2, Art 3, Art 4, Art 5 | Medium | TODO: Check again. Very Important. Learned new things |
| 03 | 173. Binary Search Tree Iterator | Python, Swift | Vid 1, Art 1 | Medium | TODO: Check again. Very Important. Learned new things |
| 04 | 281. Zigzag Iterator | Python, Swift | Art 1 | Medium | --- |
Detailed explanations with leetcode examples
Read this wiki article first.
In computational geometry, a sweep line algorithm or plane sweep algorithm is an algorithmic paradigm that uses a conceptual sweep line or sweep surface to solve various problems in Euclidean space. It is one of the key techniques in computational geometry. The idea behind algorithms of this type is to imagine that a line (often a vertical line) is swept or moved across the plane, stopping at some points. Geometric operations are restricted to geometric objects that either intersect or are in the immediate vicinity of the sweep line whenever it stops, and the complete solution is available once the line has passed over all objects.
Sweep line algorithms are used in solving planar problems. The basic outline of a sweep line algorithm is as follows:
-
Sweep a line across problem plane.
-
As the line sweeps across the plane, events of interest occur, keep track of these events.
-
Deal with events that occur at the line leaving a solved problem behind.
- [To be written]
| # | Title | Solution | Tutorial | Level | Remarks |
|---|---|---|---|---|---|
| 01 | 1272. Remove Interval | Python | Art 1 | Medium | Line Swap |
| 02 | 1288. Remove Covered Intervals | Python | Art 1 | Medium | Line Swap with Greedy. A must read solution. A gold mie, learned a lot |
| 03 | 1229. Meeting Scheduler | Python | Art 1 | Medium | Line Swap, learned a lot |
| 04 | 850. Rectangle Area II | Python | Art 1, Vid 1, Art 2 | Hard | Line Swap using heap and Segmet Tree. TODO: Solve it using Segment Tree |