Add analytical azimuth method to solarposition.py. #349

veronicaguo · 2017-07-14T22:58:22Z

Addresses issue #291

wholmgren

Thanks @veronicaguo, and sorry for forgetting to review this until now. It mostly looks good to me. It needs:

tests similar to these
an entry in the api.rst file.
an entry in the latest 0.4.6 whatsnew file.

@mikofski wrote the closely related functions, so it would be nice if he could review as well.

wholmgren · 2017-07-24T16:42:35Z

pvlib/solarposition.py

+    [2] J. H. Seinfeld and S. N. Pandis, "Atmospheric Chemistry and Physics"
+    p. 132, J. Wiley (1998)
+
+    `Wikipedia: Solar Azimuth Angle <https://en.wikipedia.org/wiki/Solar_azimuth_angle>`_


reference needs a number

wholmgren · 2017-07-24T16:42:41Z

pvlib/solarposition.py

+
+    `Wikipedia: Solar Azimuth Angle <https://en.wikipedia.org/wiki/Solar_azimuth_angle>`_
+
+    `PVCDROM: Azimuth Angle <http://www.pveducation.org/pvcdrom/2-properties-sunlight/azimuth-angle>`_


Not as accurate when azimuth angle is close to due north.

veronicaguo · 2017-07-24T22:37:38Z

Thanks @wholmgren, I have made some updates to the method and test. The method is quite accurate when the sun is away from the north. The doc files are complete now.

wholmgren

I have a few concerns about the test (below), but otherwise this looks good.

wholmgren · 2017-07-25T15:30:41Z

pvlib/test/test_solarposition.py

+    zenith = solarposition.solar_zenith_analytical(lat_rad, hour_angle, decl)
+    azimuth_2 = solarposition.solar_azimuth_analytical(lat_rad, hour_angle,
+                                                       decl, zenith)
+    for idx, a in enumerate(azimuth_1):


Can you add some comments as to why you've structured the for loop and the assert statements this way? Please also replace a with something more descriptive such as azi or azimuth.

Sure. The analytical azimuth formula is quite accurate in every direction, with an error or 1-2 degrees, except when the sun is in the north. So I separated those cases out through the for loops and if statements and gave them different atol values. Also, since the sun is only in the north during midnight when no power is produced, it shouldn't impact solar performance calculations. The test code is not in the most concise form right now. I will try slim it down a bit. Thank you for the feedback.

wholmgren · 2017-07-25T15:32:34Z

pvlib/test/test_solarposition.py

+    for idx, a in enumerate(azimuth_1):
+        if a < 0.7:
+            assert np.allclose(a, solar_azimuth[idx], atol=0.025) or \
+                   np.allclose(a + np.pi * 2, solar_azimuth[idx], atol=0.55)


atol=0.55 implies an accuracy of 32 degrees, correct? That seems quite bad. Not sure if the test needs to change or if that's a limitation of the algorithm under some input parameters.

atol=0.55 only when the sun is in the north, which is every night from 12-1 AM. It is otherwise quite accurate during the rest of the day. I assume it's probably a limitation with the analytical method that most references share.

In case a system in the Southern hemisphere is analyzed, the sun will be in the North during the day. Shouldn't the code also be able to correctly handle this case?

Thanks @trichrt for pointing it out. The analytical formula actually takes care of it inherently. When in the Southern hemisphere, the calculation is less accurate when the sun is in the south during midnight. The current test is for a Northern hemisphere location. I can put together a test for Southern hemisphere if desired.

In that case we should restrict the atol=0.55 tests to azimuth angles that are close to 0/360 (as defined by the more accurate models).

Agreed. The discrepancies start to appear within a 30-degree range around 0/360, i.e. from 345 to 15 degree. Have updated the azimuth threshold in the latest commit.

wholmgren · 2017-07-26T21:14:17Z

I just noticed that you're testing a year of data with for loops. How long does this take to run? A couple of np.testing.assert_allclose calls might be a lot faster and more readable.

veronicaguo · 2017-07-26T23:32:13Z

I'm using for loops to run the assert statements on each of the results one by one, and the np.allclose call doesn't allow for that. It takes ~0.06s to run the loops.

With the threshold azimuth being 0.275, discrepancies start to appear between the analytical and spa methods, but there are results smaller than 0.275 and yet still are very accurate. It is determined by the time of the year. The greatest discrepancy is observed around late January. So np.allclose doesn't work in this case, and also assert statements need to be separated for results that span across 0/360.

On that note, a test on a Southern hemisphere location wouldn't require the loops since azimuths around 180/360 don't run across 0. Therefore, a few np.allclose calls would work here. Would you prefer that?

mikofski · 2017-07-26T23:43:53Z

You could use also just use np.where to make a logical mask to filter out the desired azimuth to test.

bad = np.where(azimuth > 0.7)
assert np.allclose(azimuth[bad], spa_az[bad], 0.55)
good = ~bad
assert np.allclose(azimuth[good], spa_az[good], 0.025)

veronicaguo · 2017-07-27T00:01:16Z

Thanks @mikofski. The thing is that you cannot put a hard cut on a single value. For example, say the azimuth is evaluated to be 0.2 at one timestamp, and the real azimuth is 6.22. This case it would need a 2*pi correction as well as atol=0.55. But at a different timestamp, the analytical method may still give 0.2 when the real azimuth is 0.213 depending on the time of the year. Now it should be tested with the other assert statement with atol=0.025. That's why I used the logical or when below the threshold. And with that, evaluations need to be timestamp by timestamp, therefore the for loop... Hope that makes sense.

wholmgren · 2017-07-27T00:44:00Z

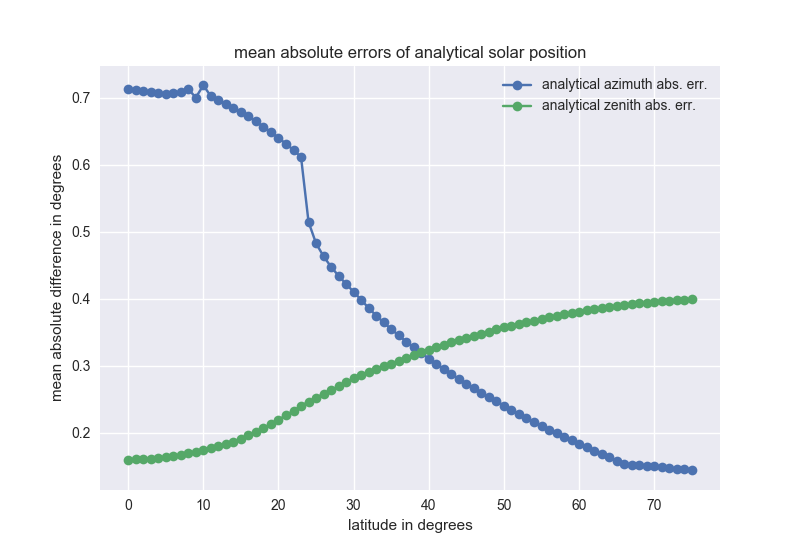
That is plenty fast.

What is the maximum azimuth angle error as a function of latitude? I'd also like to know this for the related functions and update the documentation accordingly. I think we can restrict the question to times at which the sun is above the horizon.

Loops no longer needed.

veronicaguo · 2017-07-27T18:52:08Z

Just updated the test to restrict to times when the sun is above horizon. It makes more sense and gets rid of the loops.

For the error as a function of latitude, it is very minimal below 66 deg lat and picks up from there pole-ward, for both Spencer and PVCDROM methods. Each data point is an average over the entire year at that latitude.

wholmgren · 2017-07-31T18:30:43Z

Thanks for the plots and the updated tests. I would not have expected that shape.

I'll merge tomorrow unless anyone has further comments.

veronicaguo · 2017-08-01T16:11:43Z

Thanks @wholmgren ! I was not expecting that shape either...

mikofski · 2017-08-09T08:24:19Z

I think I can explain the surprising discontinuity in azimuth abs. error going north.

TL;DR: The errors are exaggerated during the summer when azimuth near zero is actually likely, if one calculation is close to zero, but the other is closer to 360. Even though these azimuths are actually very close, their absolute difference is quite large! To evaluate the real absolute error, I just shifted all azimuth from 0-360 scale to the equivalent -180 to 180 scale. EG: 2 is still 2, but 358 would be -2.

With the correctly shifted scale, the errors are more reasonable, although there are still some surprising discontinuities!

analytical azimuth abs. err. mean < 4%
analytical zenith abs. err. mean < 1%

stats:

>>> np.abs(sp[['az_reldiff_shift', 'ze_reldiff']][sp.daytime]).describe()

	az_reldiff_shift	ze_reldiff
count	4.462000e+03	4462.000000
mean	3.574673e-02	0.005356
std	3.120498e-01	0.002516
min	3.454106e-07	0.000003
25%	5.346862e-04	0.003387
50%	1.108402e-03	0.005946
75%	2.086851e-03	0.007427
max	1.225220e+01	0.009280

Figure 1: latitude vs. absolute_error = abs(1 - azimuth / analytical_azimuth) (dimensionless)

Figure 2: error distribution

Figure 3: If I don't shift the azimuth I get the same discontinuity as @veronicaguo

Figure 4: you can see errors are concentrated in summer, which is when the very long days occur - I had looked at July 1st at 70 degrees and already seen the large (northern) azimuths at sunrise/sunset, but it didn't occur to me until I saw this distribution

I evaluated all northern latitudes from 0 - 75 in 1 degree increments for hourly data and removed all hours for which zenith > 90.

from pvlib.solarposition import (
    solar_azimuth_analytical, get_solarposition, solar_zenith_analytical,
    hour_angle, declination_spencer71, equation_of_time_spencer71
)
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
plt.ion()

dt = pd.DatetimeIndex(start='2017-01-01T00:00:00-0800',
                      end='2017-12-31T23:59:59-0800', freq='H')

LAT = np.arange(0, 76, 1.0, dtype=float)
LON = -120
abserr = []
abserr_shift = []

for lat in LAT:
    sp = get_solarposition(time=dt, latitude=lat, longitude=LON)

    decl = declination_spencer71(dt.dayofyear)  # radians
    eot = equation_of_time_spencer71(dt.dayofyear)  # minutes
    hr = hour_angle(times=dt, longitude=LON, equation_of_time=eot)  # degrees

    ze = solar_zenith_analytical(np.radians(lat), np.radians(hr), decl)
    az = solar_azimuth_analytical(np.radians(lat), np.radians(hr), decl, ze)

    sp['analytical_zenith'] = np.degrees(ze)
    sp['analytical_azimuth'] = np.degrees(az)
    sp['daytime'] = sp['zenith'] < 90.0

    sp['az_reldiff'] = 1 - sp['azimuth'] / sp['analytical_azimuth']
    sp['ze_reldiff'] = 1 - sp['zenith'] / sp['analytical_zenith']
    abserr.append(np.abs(sp[['az_reldiff', 'ze_reldiff']][sp.daytime]).mean())

    sp['shift_sphere_az'] = (
        (sp.analytical_azimuth - 360)*(sp.analytical_azimuth > 180) +
        sp.analytical_azimuth*(sp.analytical_azimuth<=180)
    )
    sp['shift_az'] = ((sp.azimuth - 360)*(sp.azimuth>180) +
                       sp.azimuth*(sp.azimuth<=180))
    sp['az_reldiff_shift'] = 1 - sp['shift_az'] / sp['shift_sphere_az']
    abserr_shift.append(np.abs(sp[['az_reldiff_shift', 'ze_reldiff']][sp.daytime]).mean())

plt.figure()
plt.plot(LAT, abserr, '-o')
plt.legend(['analytical azimuth abs. err.', 'analytical zenith abs. err.'])

np.abs(sp[['az_reldiff', 'ze_reldiff']][sp.daytime]).plot()

plt.figure()
plt.plot(LAT, abserr_shift, '-o')
plt.legend(['analytical azimuth shift abs. err.', 'analytical zenith abs. err.'])

np.abs(sp[['az_reldiff_shift', 'ze_reldiff']][sp.daytime]).plot()

mikofski · 2017-08-09T09:09:05Z

pvlib/solarposition.py

+    hour_angle
+    solar_zenith_analytical
+    """
+    return np.sign(hour_angle) * np.abs(np.arccos((np.cos(zenith) * np.sin(


@veronicaguo and @wholmgren sorry for super late review, and just a tiny nitpick, but I don't think np.abs is necessary here because according to numpy documentation on np.arccos it is only defined from on [0, pi]

The angle of the ray intersecting the unit circle at the given x-coordinate in radians [0, pi].

Therefore, it will never return a negative number, so no need for absolute value.

adriesse · 2017-08-09T09:20:38Z

Very interesting. Perhaps something like this could be used to compare angles:

def angle_difference(a1, a2):
    da = a2 - a1
    da = np.where(da > 180, da-360, da)
    da = np.where(da<=-180, da+360, da)
    return da

mikofski · 2017-08-09T09:28:49Z

Your script Fu is definitely better than mine! Nice use of np.where()!

Let me be clear, there is no need to change these angles at all. I only shifted them for the comparison because of the issue I described where errors were exaggerated because one azimuth was near zero and the other calculation was near 360

adriesse · 2017-08-09T09:45:06Z

I understand the shift is just for the comparison, but it moves the comparison problem to the South, doesn't it?

mikofski · 2017-08-09T13:58:19Z

Ah, yes! Now errors where one azimuth is close to -180 and the other is closer to 180 form discontinuities. Now I understand your formulation. I will recalculate abs error with your expression and see if that removes all discontinuities. Thanks!

mikofski · 2017-08-09T17:55:36Z

absolute errors for analytical functions

mean analytical azimuth abs. err. < 1.3%
mean analytical zenith abs. err. < 1.2%

recalculation with better shifting of angle difference

OK, using @adriesse magic script fu has significantly improved the absolute error calculations, although there are still two (2) surprise discontinuities, they occur in both zenith and azimuth absolute errors, so it may be a machine precision or other mathematical/computational limitation, and I'm not going to worry about it.

The distribution still shows a pretty massive spike in summer for azimuth, what could it be, I can't think about it right now, perhaps someone will figure out that it's totally obvious and tell me.

the new abs error with script magic by @adriesse

from pvlib.solarposition import (
    solar_azimuth_analytical, get_solarposition, solar_zenith_analytical,
    hour_angle, declination_spencer71, equation_of_time_spencer71
)
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
plt.ion()

dt = pd.DatetimeIndex(start='2017-01-01T00:00:00-0800',
                      end='2017-12-31T23:59:59-0800', freq='H')

LAT = np.arange(0, 76, 1.0, dtype=float)
LON = -120
abserr = []

# this is the magic by Anton Driesse, to detect where to shift the circle
def angle_difference(a1, a2):
    da = a2 - a1
    da = np.where(da > 180, da-360, da)
    da = np.where(da<=-180, da+360, da)
    return da


for lat in LAT:
    sp = get_solarposition(time=dt, latitude=lat, longitude=LON)

    decl = declination_spencer71(dt.dayofyear)  # radians
    eot = equation_of_time_spencer71(dt.dayofyear)  # minutes
    hr = hour_angle(times=dt, longitude=LON, equation_of_time=eot)  # degrees

    ze = solar_zenith_analytical(np.radians(lat), np.radians(hr), decl)
    az = solar_azimuth_analytical(np.radians(lat), np.radians(hr), decl, ze)

    sp['analytical_zenith'] = np.degrees(ze)
    sp['analytical_azimuth'] = np.degrees(az)
    sp['daytime'] = sp['zenith'] < 90.0

    sp['az_reldiff'] = angle_difference(sp['azimuth'], sp['analytical_azimuth']) / sp['azimuth']
    sp['ze_reldiff'] = 1 - sp['zenith'] / sp['analytical_zenith']
    abserr.append(np.abs(sp[['az_reldiff', 'ze_reldiff']][sp.daytime]).mean())

plt.figure()
plt.plot(LAT, abserr, '-o')
plt.legend(['analytical azimuth abs. err.', 'analytical zenith abs. err.'])

np.abs(sp[['az_reldiff', 'ze_reldiff']][sp.daytime]).plot()

wholmgren · 2017-08-09T18:15:19Z

Interesting. Thanks @mikofski and @adriesse for following up. This is great info for future reference. We might consider pulling some of this into the official documentation at some point.

adriesse · 2017-08-09T18:53:34Z

Ok, now I see more clearly what you are doing: "absolute error" means "absolute value of the relative error". This gets you in trouble when the zenith is at or near zero, which happens at latitudes < 23. The other trouble when the zenith is very small is that a small change in sun position along the path of the sun creates a large change in azimuth angle.

I think you should be looking at degree differences rather than percentage difference, and even that won't fix the latter problem. I also suggest running this at minute rather than hourly intervals and/or pick fixed intervals of solar time and I think you will lose some of the funny stuff.

mikofski · 2017-08-09T19:33:33Z

Good point, I'll redo in degrees, I like non dimensional better, but you're right of course about over exaggerating differences of very small numbers. Also usually instead of abs() I prefer RMS, but I was trying to follow the previous calculations already in this thread

mikofski · 2017-08-09T20:24:14Z

@adriesse in degrees, abserr = abs(angle_difference(a1, a2)[daytime]).mean() , azimuth max mean abs. error is around 0.7° close to the equator and zenith max mean abs. error is around 0.4° close to the north & south poles.

using 180° to scale azimuth angle differences and 90° to scale zenith I get these scaled/non-dimensionalized absolute errors, using abs(angle_difference(a1,a2)[daytime]/scale).mean()

mikofski · 2017-08-09T20:27:40Z

@wholmgren surprisingly accurate, but the zenith still doesn't account for atmospheric refraction, and that error isn't included here.

Add analytical azimuth method.

52cfb3b

wholmgren reviewed Jul 24, 2017

View reviewed changes

wholmgren added this to the 0.4.6 milestone Jul 24, 2017

wholmgren added the enhancement label Jul 24, 2017

veronicaguo added 6 commits July 24, 2017 10:27

Number linked references.

5395164

Add test for solar_azimuth_analytical.

4e56576

Add an entry in the api.rst file.

c0698d4

Correct for different azimuth convention.

e3c7530

Update test tolerance.

9c2b89b

Not as accurate when azimuth angle is close to due north.

Added an entry in the v0.4.6 whatsnew file.

b6d6fb9

wholmgren reviewed Jul 25, 2017

View reviewed changes

Update assert statements.

d1b38b5

Update threshold for atol=0.55 assert statement.

2c346c4

veronicaguo added 2 commits July 27, 2017 10:20

Merge branch 'master' of github.com:pvlib/pvlib-python

3728f15

Update test, only when the sun is above horizon.

31bf30d

Loops no longer needed.

wholmgren merged commit 16c6eac into pvlib:master Aug 1, 2017

wholmgren mentioned this pull request Aug 7, 2017

Simple analytical Azimuth method #291

Closed

wholmgren modified the milestones: 0.4.6, 0.5.0 Aug 8, 2017

mikofski reviewed Aug 9, 2017

View reviewed changes

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Add analytical azimuth method to solarposition.py. #349

Add analytical azimuth method to solarposition.py. #349

veronicaguo commented Jul 14, 2017

wholmgren left a comment •

edited

Loading

wholmgren Jul 24, 2017

wholmgren Jul 24, 2017

veronicaguo commented Jul 24, 2017

wholmgren left a comment

wholmgren Jul 25, 2017

veronicaguo Jul 25, 2017

wholmgren Jul 25, 2017

veronicaguo Jul 25, 2017

timorichert Jul 25, 2017

veronicaguo Jul 25, 2017

wholmgren Jul 26, 2017

veronicaguo Jul 26, 2017

wholmgren commented Jul 26, 2017 •

edited

Loading

veronicaguo commented Jul 26, 2017 •

edited

Loading

mikofski commented Jul 26, 2017

veronicaguo commented Jul 27, 2017

wholmgren commented Jul 27, 2017

veronicaguo commented Jul 27, 2017 •

edited

Loading

wholmgren commented Jul 31, 2017

veronicaguo commented Aug 1, 2017

mikofski commented Aug 9, 2017 •

edited

Loading

mikofski Aug 9, 2017

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017

wholmgren commented Aug 9, 2017

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017


		`Wikipedia: Solar Azimuth Angle <https://en.wikipedia.org/wiki/Solar_azimuth_angle>`_

		`PVCDROM: Azimuth Angle <http://www.pveducation.org/pvcdrom/2-properties-sunlight/azimuth-angle>`_

Add analytical azimuth method to solarposition.py. #349

Add analytical azimuth method to solarposition.py. #349

Conversation

veronicaguo commented Jul 14, 2017

wholmgren left a comment • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

veronicaguo commented Jul 24, 2017

wholmgren left a comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

wholmgren commented Jul 26, 2017 • edited Loading

veronicaguo commented Jul 26, 2017 • edited Loading

mikofski commented Jul 26, 2017

veronicaguo commented Jul 27, 2017

wholmgren commented Jul 27, 2017

veronicaguo commented Jul 27, 2017 • edited Loading

wholmgren commented Jul 31, 2017

veronicaguo commented Aug 1, 2017

mikofski commented Aug 9, 2017 • edited Loading

Choose a reason for hiding this comment

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017

absolute errors for analytical functions

recalculation with better shifting of angle difference

wholmgren commented Aug 9, 2017

adriesse commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017

mikofski commented Aug 9, 2017

wholmgren left a comment •

edited

Loading

wholmgren commented Jul 26, 2017 •

edited

Loading

veronicaguo commented Jul 26, 2017 •

edited

Loading

veronicaguo commented Jul 27, 2017 •

edited

Loading

mikofski commented Aug 9, 2017 •

edited

Loading