Change histogram SQL query to use linspaced sampling #1022
Conversation
| ) | ||
| /* Ensure we omit reserved rows, which have NULL step values. */ | ||
| WHERE series = :tag_id AND step IS NOT NULL | ||
| /* Bucket rows into sample_size linearly spaced buckets, or do |
There was a problem hiding this comment.
Thanks a lot for the lucid comments.
| WHERE series = :tag_id AND step IS NOT NULL | ||
| /* Bucket rows into sample_size linearly spaced buckets, or do | ||
| no sampling if sample_size is NULL. */ | ||
| GROUP BY |
There was a problem hiding this comment.
If I'm understanding correctly, this GROUP BY makes it so that we only sample 1 event at each sampled step, right? ie, either the min or max per bucket that you had noted earlier.
There was a problem hiding this comment.
Yeah, the GROUP BY basically partitions the series by a "bucket index" so that we divide the range into k - 1 even sized intervals, and then within each interval we take the minimum aka first step in that interval. The way we do the math, the max step is always assigned to its own singleton interval with bucket index k - 1, so it also get selected basically as the lower bound of a kth interval that just happens not to contain any other steps (so conceptually, I think of the selected steps as being the set of lower and upper bounds of k - 1 intervals instead).
There was a problem hiding this comment.
Note also that if the sample_size is null, we effectively set it to max_step - min_step + 1 which is the total number of distinct steps. As it happens that means our formal now has (max_step - min_step) in both numerator and denominator, so they cancel and each step gets assigned a unique bucket index of step - min_step.
If sample_size is greater than the total number of steps, the bucket index for each step is assigned as m * step + C where m > 1, so each step will still get a unique bucket index and hence all steps will be selected.
This replaces the randomized downsampling used in the histograms plugin SQL query with a systematic linear sampling strategy, based on dividing the range into k - 1 equal-sized intervals and then returning the lowest steps at or above the k interval boundaries. This produces cleaner and more readily understandable/predictable charts, where we now get the nice property that (at least when steps are contiguous) any two adjacent histogram curves will be separated by the same step delta +/- 1 so the actual rate of change is easier to discern. As a bonus, the new results also always include the lowest and highest steps in the series.
Old sampling:
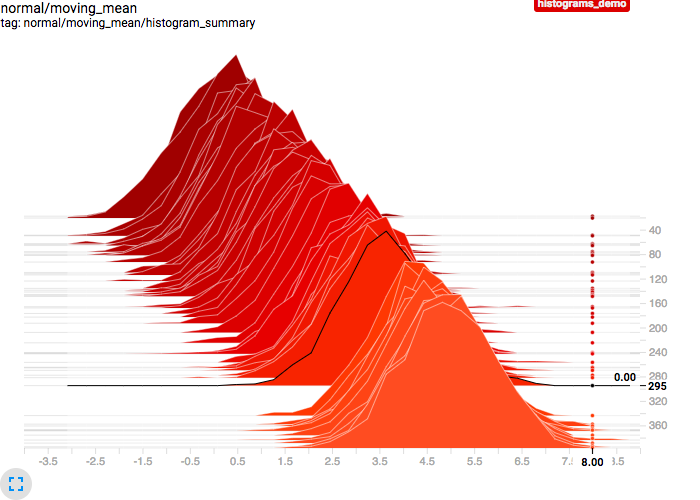
New sampling:
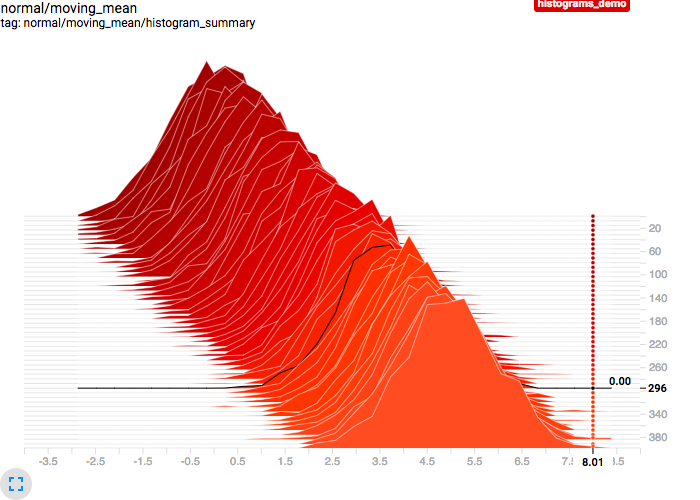
We can now turn off sampling inline with the same query rather than using string templating. I factored out finding the tag ID into a separate query since it's used twice in the main query, but we could put that query in a WITH clause and then read it with two inline scalar queries to keep it all in one query, if that's preferred. I expect that performance-wise this query should be similar to the randomized one (they're both essentially O(n) in series length). An alternate approach would be computing the k interval boundaries directly (either in python or with a recursive WITH query) and then using correlated subqueries to fetch each result individually, which would theoretically be O(k log(n)). That would in theory be more efficient when k < n/log(n), though I expect the constant factors dominate until n gets fairly large, so we'd want to do some experimental testing.
I bumped the histogram sample size from 50 to 51 because N+1 samples correspond to N intervals, so making N a round number makes the step counts more likely to be round numbers. I also set the distributions plugin to use a sample size of 501 (current reservoir size + 1) since we want an upper bound on the number of points returned even if running against an unsampled DB.